Optics to the Time of Kepler

In 1604 Johannes Kepler published a treatise with the unprepossessing title, “A Supplement to Witelo” ( Ad Vitellionem Paralipomena ). The titular “Witelo” was representative of a group of late thirteenth-century optical theorists—the so-called perspectivists—whose account of light and sight was considered so definitive that it assumed paradigmatic status from rough 1300 until well into the seventeenth century. If, therefore, we take Kepler at his word, all he meant to do in the Paralipomena was round out this account with some additional material, not undermine it to its very core. Yet, in fact, that is precisely what he did. In the process he helped lay the foundations of modern physical optics.

The key point of conflict between Kepler and the perspectivists lay in their interpretation of the eye and its function in the visual act. Kepler, who proposed the theory of retinal imaging in chapter 5 of the Paralipomena , was convinced that the eye operates like a camera obscura . Accordingly, he argued that the pupil channels the light radiating from every point in the field of view onto the front surface of the crystalline lens. The lens, in turn, refractively focuses that light to corresponding points on the retina at the back of the eye. In so doing, it projects a real, reversed and inverted image (or “painting” [ pictura ] in Kepler’s terminology) of the objective source on the retinal screen.

By contrast, the theory championed by Witelo and his perspectivist compeers has the crystalline lens visually sense the rays of light that impinge directly upon its surface along the orthogonal. The rest it simply ignores. Out of all these sensed impingements it forms a point-by-point virtual representation ( forma or species in medieval parlance) of the objective source of the light and luminous color. Such virtual representations are then conveyed by means of an physico-physiological process through the rest of the eye to the hollow optic nerve at the back and thence into the brain for perceptual and intellectual scrutiny. Unlike Kepler’s picturae , which are objectively realized on the retina, these images have no actual existence until they are subjectively realized in the eye and brain.

Some manifest, some not, the differences between these two theories and the implications of those differences for the development of post-Keplerian optics need not detain us at this point. For now, it is enough to say that they are significant and that they are the result of a long, complicated, and uneven path of theoretical development harking back to classical antiquity. It is therefore our purpose in what follows to trace that path with the aim, ultimately, of making sense of both the perspectivists’ paradigmatic theory and Kepler’s revolutionary reaction to it.

Accordingly, we will begin with a look at early attempts to place the study of sight and light on a scientific footing during Greco-Roman antiquity, primarily on the basis of ray-theory and a coherent anatomical and physiological model of the ocular system. Ptolemy (d. c. 180 CE) and Galen, (d. c. 230 CE) played key roles in this development. We will then examine how Greco-Roman visual theory, with its foundations in ray analysis and Galenic anatomy and physiology, was adopted and modified by Arabic thinkers, among whom Avicenna (d. 1037) and Ibn al-Haytham (d. 1040/41) figure prominently. Next, we will turn to the medieval Latin West in order to see how the perspectivists constructed their visual paradigm on the basis of earlier optical theorists, Ibn al-Haytham in particular. Finally, we will conclude with a look at certain technological and theoretical developments during the Renaissance that paved the way for Kepler’s revolutionary theory of retinal imaging.

The Classical Foundations: 400 BCE to 200 CE

Three basic theories of vision were offered in Greek antiquity. According to one, the eye sends a rarefied flux out to objects in order to make visual contact with them. This alternative is commonly referred to as “extramissionist.” A second alternative, referred to as “intromissionist,” assumed the opposite: namely, that objects send something into the eye, which then interprets the information conveyed to it visually, perceptually, and intellectually. The third alternative was a hybrid of the two. An example of this alternative can be found in the Timaeus , where Plato (d. 347 BCE) claims that the eye emits a subtle, non-burning fire that mingles in the air with the external fire of sunlight to reach out to external objects. These objects, in turn, emit particles of various sizes into the ocular fire, thereby causing it to dilate or contract. The resulting dilations and contractions are interpreted as colors, depending on the size of particles causing them, the extreme of each being construed as white and black. ¹ Much later, the renowned medical writer Galen (d. c. 200 CE) proposed a similar theory, according to which the eye emits pneuma, a mixture of fire and air, into the surrounding sunlit air, which the ocular pneuma then transforms into a percipient extension of the eye. In contact with this pneumatized air, objects convey visual information back through it into the eye for sensitive, perceptual, and intellectual processing.

For the pure, intromissionist alternative, we look to Aristotle (d. 322 BCE), who offered a fairly detailed account of vision in On the Soul and On Sense and What Is Sensed . As he explains it, the key to seeing lies in there being a continuous transparent medium, such as air, between the eye and external objects. This medium provides uninterrupted physical contact between the two. It is not inherently transparent, though. It is only potentially so. In order to become actually transparent, it needs the presence of light, which renders it capable of taking on the color of surrounding objects in a qualitative way. Transmitted instantaneously through the qualitatively transformed medium to the eye, the color is seen by assimilation. Aristotle likens such assimilation to the impression of a seal in soft wax, and it is from this impression that the perceptual faculty infers such things as the shape, size, distance, and so forth of its source object. For Aristotle, therefore, color is the primary, and indeed sole, object of sight. The remaining visible qualities are secondary and inferential. ²

The Basis of the Classical Visual Ray Theory

The most obvious example of the extramissionist alternative is the visual ray theory at the heart of Euclid’s Optics and Catoptrics (c. 300 BCE), Hero of Alexandria’s Catoptrics (c. 60 CE), and Ptolemy’s Optics (c. 160 CE). It was upon this theory that the geometrical analysis of optics was based, and it was out of this analysis and the laws underlying it that a significant body of knowledge about reflection and refraction was developed. It is important to note, however, that at its inception with Euclid, and subsequently with Hero, the visual ray theory was limited to explaining how we perceive the spatial characteristics of external objects, whether by means of unimpeded lines of sight or by means of reflection from polished bodies. Neither Euclid nor Hero mentioned the perception of light or color, and neither was concerned with how the visual system processes visible information.

At the analytic core of the Euclidean visual ray theory is the visual cone, which comprises a bundle of innumerable rectilinear lines of flux emanating from a vertex-point within the eye, presumably at its center. Passing out through the pupil and thus circumscribed by it, this conical bundle of rays extends outward into the surrounding space, its base defining the field of view for each eye. Whatever lies within that field of view and is opaque enough to block any of the cone’s constituent rays is visually sensed in a way analogous to that in which outstretched fingers tactilely sense solid external objects. ³ This sense of visual touch allows us to see the shape of things, discern their separation from one another, and judge their distance away from us. For instance, in the case of direct, unimpeded vision, if I want to know the height of upright object AB at known distance DB from my eye at D, in figure 1, all I need do is place object ZE of known height upright between AB and my eye such that its top point Z blocks my sight of top point A of AB. Then, having measured DE, I can calculate AB according to the similarity of triangles DZE and DAB. ⁴

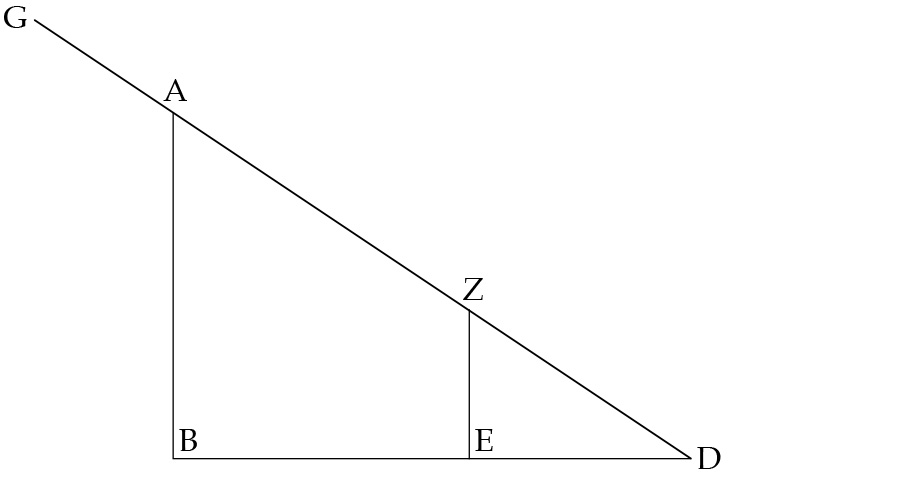
Figure 1: Determining the height of an object according to Euclidean visual ray theory. Smith, From Sight to Light .

As is obvious from this example, the rectilinearity of visual rays is key to their usefulness in the geometrical analysis of sight. But why assume such rectilinearity? To be sure, there are clear practical reasons to make that assumption, but at a deeper level the answer lies in the principle of natural efficiency, which is summed up in the Aristotelian dictum that nature does nothing in vain. All natural actions will therefore occur as efficiently as possible, barring abnormal constraints. This means that the radiation of visual flux, being natural, must, under normal, unconstrained circumstances, follow the shortest point to point distance, which is a straight line.

Hero of Alexandria extends this principle to reflection, which, as mentioned above, is subject to the law of equal angles. According to this law, when a ray strikes a polished surface at a given angle, it will reflect at an equal angle. As proof of the validity of this law, Hero appeals to the principle of least lines.

Figure 2: Demonstration of the law of equal angles. Smith, From Sight to Light .

Let AB in figure 2 be a plane mirror and CD a convex spherical mirror tangent to it at point R. Assume that a visual ray from point E radiates along ER to strike both mirrors at R, thus forming angle of incidence ERB with the mirrors’ surfaces. Let ER reflect from R along RO to form angle of reflection ORA equal to angle of incidence ERB. Now assume that the visual ray from E follows path ER’ to form angle of incidence ER’B and then reflects from R’ along R’O to form angle of reflection OR’A. Clearly in this case angle of incidence ER’B ≠ angle of reflection OR’A. That the light must follow combined path ER,RO rather than combined path ER’,R’O is dictated by the fact that ER + RO < ER’ + R’O. In fact, ER + RO is less than any other combined path, so the path dictated by the equal angles law is the most efficient possible. The same holds mutatis mutandis for the convex mirror. ⁵

In tandem with the principle of natural efficiency, the law of equal angles suggests a simple method of determining image location in reflection. This method depends on the cathetus rule, which locates the image along a straight line dropped perpendicularly from the object to the reflecting surface (the so-called cathetus). Where this perpendicular meets the extension of the incident visual ray from the eye is where the image lies.

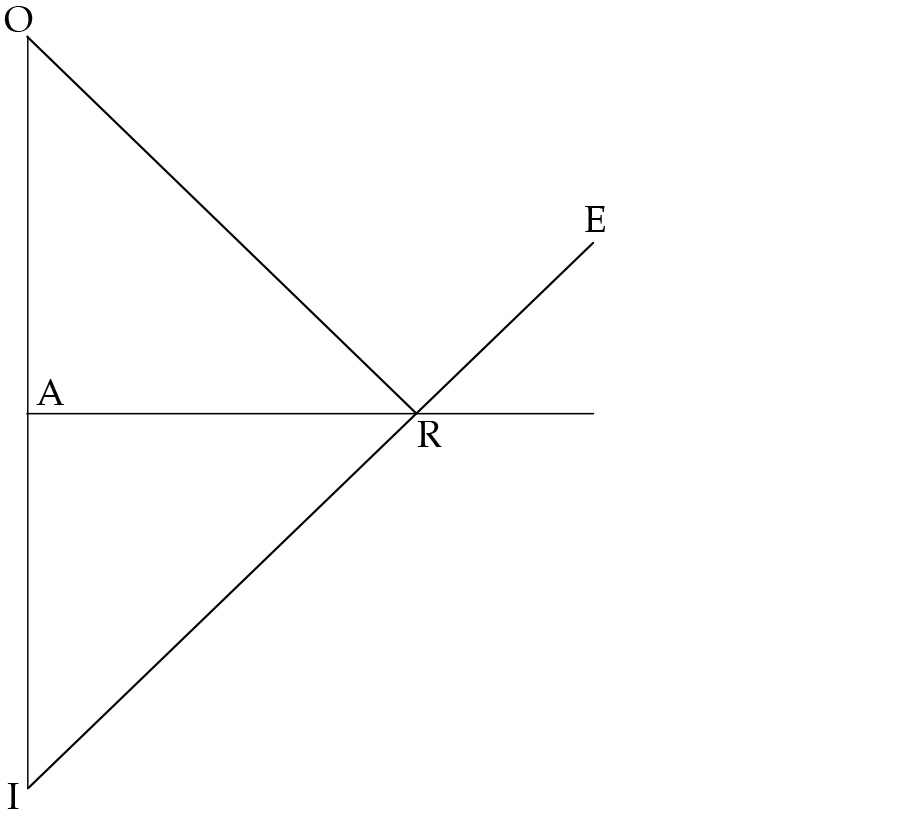
Figure 3: The law of equal angles used to determine the location of an image in a mirror. Smith, From Sight to Light .

For instance, let AR in figure 3 be a plane mirror, ER a visual ray emanating from the eye at E and incident at point R on the mirror, and ray RO the ray reflected to the object at O. Drop cathetus OA perpendicular to the mirror’s surface, and extend it in a straight line below that surface along AI. Meanwhile, extend visual ray ER below the mirror in a straight, continuous line until it meets the extension of cathetus OA at point I. Point I is therefore where point O will be seen by the eye located at E, and it will appear precisely the same distance below the mirror’s surface as it actually lies above it. The same analysis applies to convex and concave mirrors, the cathetus in both cases passing from the object to the center of the mirror’s curvature.

The Theoretical Grounds of Ptolemy’s Optical Analysis

The account of direct vision and reflection provided in Euclid’s Optics and Catoptrics , as well as in Hero of Alexandria’s Catoptrics , is fairly rudimentary, in part because of its limited analytic scope. Neither author attempted to give a comprehensive account of visual perception. Far from it, both limited themselves to explaining how we apprehend the superficial, spatial characteristics of things, making no effort to account for how we make perceptual or intellectual judgments about what we see. Ptolemy, on the other hand, was at pains to explain the actual process of visual perception not only on theoretical but also on empirical grounds. He was also aware of the limitations of ray analysis in accounting fully for that process and the consequent need to take physical and psychological factors into account.

Laid out systematically in his Optics , Ptolemy’s account of visual perception originally occupied at least five books, of which the first is currently lost and the fifth is incomplete. From what remains, however, we can infer that the first book dealt with the basic grounds of vision according to “what enables light and visual flux to interact, how they assimilate to one another, how they differ in their powers and operations, what kind of essential difference characterizes each of them, and what sort of effect they undergo.” ⁶

Having discussed these things, Ptolemy devotes the entire second book and part of the third book to the most general aspects of vision, limiting his analysis to instances in which the visual contact between eye and external objects is direct and unbroken. He begins in book 2 by describing what we see according to three levels. At the lowest level is what he describes as “luminous compactness.” By this he means that, in order to be visible at all, an object must be opaque and illuminated or self-luminous. At the next level is color, which is primarily visible insofar as it defines any opaque, illuminated surface visually. Last come the secondary visibles, which are inferred from the immediate apprehension of color, such things as “size, place, and shape [that] are perceived only through the mediation of bodies' surfaces, which coincide with the colors upon which external light falls.” ⁷ Not coincidentally, this division according to primary and secondary visibles mirrors Aristotle’s equivalent categorization in the De anima .

While clearly influenced by Aristotle’s account of visual perception, Ptolemy rejected Aristotelian intromissionism in favor of Euclidean extramissionism. Unlike Euclid, however, he conceived of the flux within the visual cone as perfectly homogeneous and continuous, not as a bundle of countless individual rays. Nonetheless, despite being homogeneous and continuous, Ptolemy’s visual flux has certain differentiating characteristics according to its disposition within the visual cone. The farther out from its source it reaches, for instance the weaker it becomes, which explains why we see distant things less clearly than closer ones. Clarity of vision is also affected by how concentrated the flux is on the object seen: the greater the concentration, the clearer the view. In addition, the flux along the visual axis, which runs from the center of the eye to the center of the visual field, yields a clearer view than that toward the cone’s edges. This explains why vision gets increasingly indistinct toward the edges of the field of view.

Where the radiated flux lies within that field allows us to determine right, left, up and down with reference to the visual axis and, ultimately, the vertex of the visual cone at the center of the eye. With reference to that point, moreover, we are able to sense how far out the flux reaches when making visual contact with moderately close objects. On that basis, we can judge their distance with fair accuracy, but lacking such sense for far away objects, we tend to misjudge their distances badly. That is why the sun and moon look roughly the same distance from us, even though the former is scores of times farther away than the latter. All told, these differentiating characteristics allow us to perceive such spatially determined things as size, shape, relative distance, relative spatial disposition, motion, and rest, all ultimately gauged by reference to the vertex of the visual cone. ⁸

Our perception of these things is often subject to error, and for a variety of reasons. If, for instance, an object lies too far away we may mistake its shape, size, or motion, as is the case with moon and sun, which appear to us as virtually immobile disks, even though they are spheres orbiting at unimaginable speeds. Such misperceptions are legion, and Ptolemy devotes considerable attention to a range of them, extending from farsightedness and nearsightedness to the oculogyral illusion and the moon illusion. ⁹ In addition to these misperceptions, Ptolemy addresses three even more fundamental sources of illusion­—diplopia (or double vision), reflection, and refraction.

Ptolemy on Binocular Vision and Diplopia

Ptolemy broaches the subject of diplopia and its basis in binocular vision fairly early in book 2, then turns to other matters, only to complete his account in book 3. Under normal circumstances, he assures us at the beginning, we are naturally inclined to bring the visual axes of both eyes to bear at the same spot on any object we look at, and if that spot is more or less in front of us, we see the entire object as single.

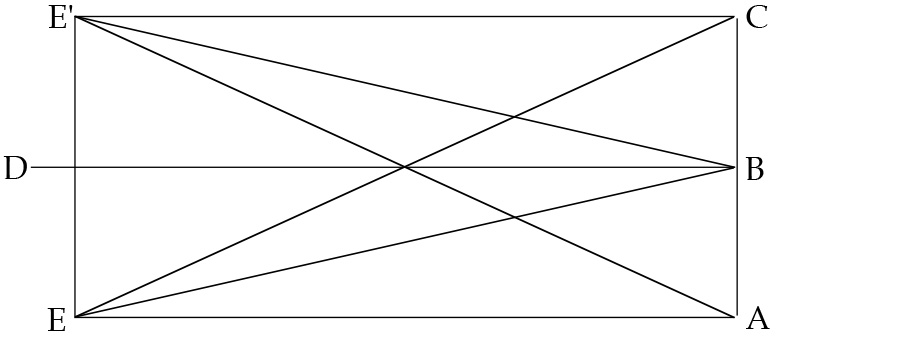
Figure 4: Ptolemy’s demonstration that the two eyes can converge on a single image under normal circumstances. Smith, From Sight to Light .

The optimal case of this situation is illustrated in figure 4, where E and E’ are the centers of the two eyes, and B represents a point on facing object AC. Line DB perpendicular to and bisecting line EE’ connecting the centers of the eyes represents the so-called common axis. If, as represented in the figure, the visual axes from both eyes converge on point B where the common axis intersects the object, then the object is seen as clearly and properly as possible according to ambient conditions (i.e., intensity of illumination, distance from the eye, and so forth). The underlying reason, according to Ptolemy, is that each point on the object to the sides of B is seen with corresponding rays (e.g., EC and E’C) that lie on the same side of, and at an equivalent distance from, the axial ray in each visual cone.

Things go awry when the two axes do not converge properly, the result being diplopia. Ptolemy details a set of experiments to illustrate this point. One such experiment is as follows. Let E and E’ in figure 5 be the vertices of the visual cones from each eye, and let the two eyes be positioned against board EE’CD to which a white peg A is placed along the common axis in front of black peg B.

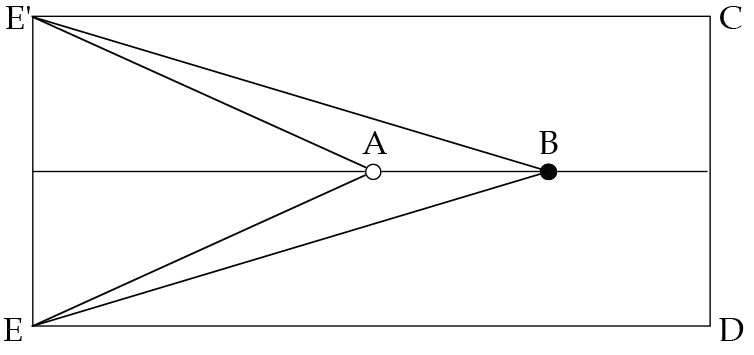
Figure 5: Ptolemy’s description of the conditions under which diplopia emerges. Smith, From Sight to Light .

First, let both visual axes converge on white peg A, but let the viewer also pay attention to black peg B. In that case, while white peg A is seen single, black peg B will appear double because it is seen with non-corresponding rays E’B, to the left of axial ray E’A, and EB to the right of axial ray EA. If, on the other hand, the two visual axes are brought to bear on black peg B, then white peg A will appear double because it is seen with non-corresponding rays E’A and EA. In both cases, the circumstances are anomalous because the visual axes are not brought to bear naturally on the appropriate point. ¹⁰

Ptolemy’s Analysis of Reflection

Whereas diplopia occurs in direct or unmediated vision, reflection involves the mediation of a polished surface, which causes visual rays that strike it to rebound. This rebound, Ptolemy asserts, is governed by the law of equal angles already established by Euclid and Hero, but this time with reference not to the reflecting surface itself but to the normal or perpendicular dropped to the point of reflection on that surface. To verify the law empirically, Ptolemy suggests we form a thin, bronze disk CBD “of moderate size” whose center point is A, as represented in figure 6. We are then to divide the disk into quadrants along BA and CAD, each of which is subdivided into 90 degrees on its outer edge (the figure shows 5° intervals).

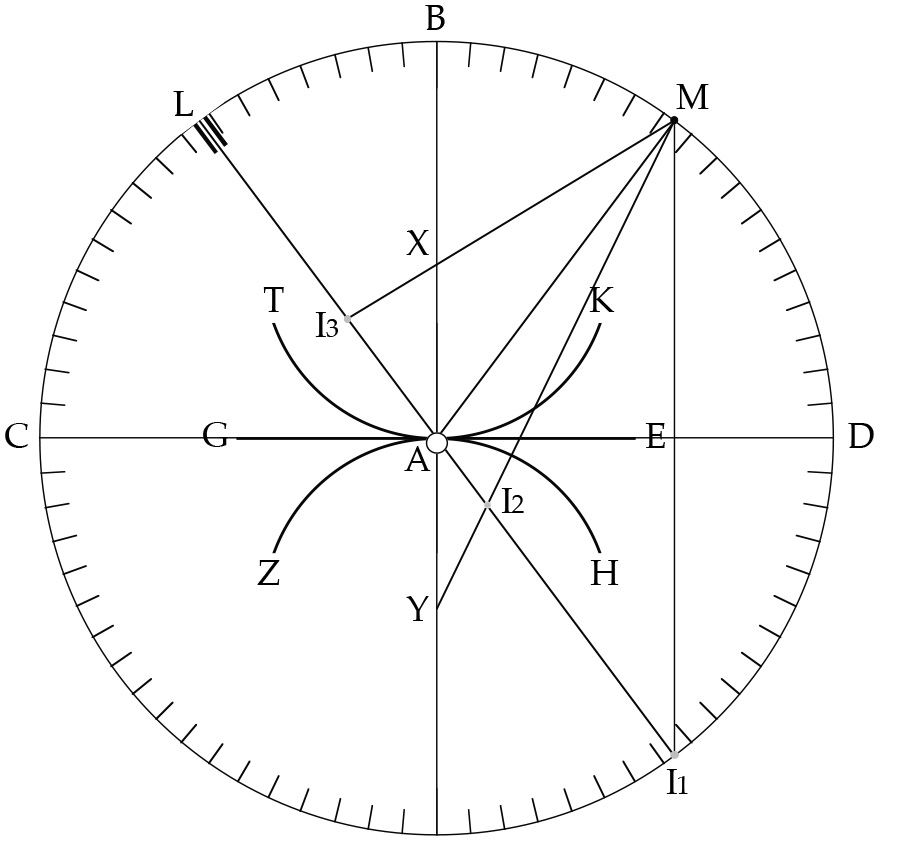
Figure 6: Diagram of Ptolemy’s apparatus for verifying the law of equal angles. Smith, From Sight to Light .

That done, we take three highly polished iron strips out of which we form three mirrors. One of these will represent a plane mirror EG to be stood upright on the disk’s surface along CD. The other two we form into circular arcs to be stood upright along TAK, and ZAH. Meantime, we are to attach two rotating arms LA and MA on to the disk, fixing them at center point A. At endpoint L of arm LA, we attach a sighting device to narrow our line of sight as much as possible along line LA, and at endpoint M of arm MA we affix a small, colored peg.

With a small marker placed at point A, we are ready to proceed with the empirical verification. First, we stand the plane mirror along GE and then move arm MA along arc BE until the colored peg at M sits at some determinate point on it. Then we move arm LA along arc BG while peering continually through the sighting device along LA until we see the colored peg’s image line up directly with the thin marker at A at image point I ₁ . Under these conditions, we find that arc BM is equal to arc BL, and this equality applies to any placement of arc MA along BE. The same holds for the two curved mirrors placed along ZAH and TAK. In both cases, if the same protocol is followed as before so that the image of M appears in line with the marker at A (I ₂ for the convex mirror and I ₃ for the concave mirror), arcs BM and BL will prove to be equal. ¹¹

Key to this verification is the cathetus rule, which, as we saw earlier, holds that the image lies at the intersection of the cathetus and the incident ray from the eye extended through the mirror. In the case of plane mirrors, this means that the image will always lie behind the mirror’s surface at an apparent perpendicular distance equal to the actual perpendicular distance the object lies in front of that surface. Because of this apparent displacement, we misperceive the object’s location, seeing it where it is not. The same applies to convex mirrors insofar as the image is seen behind the mirror, although it appears to lie closer to its surface than the object actually lies above it. In addition to dislocation, images in convex mirrors suffer distortion in both size and shape, appearing smaller and more gibbous than their generating objects.

Things are considerably more complicated with concave mirrors, which is why Ptolemy devotes the entirety of book 4 to them. For one thing, unlike plane and convex mirrors, concave mirrors can yield more than one reflection, depending on how the eye and the object are placed with respect to the reflecting surface. In fact, as Ptolemy demonstrates, there can be as many as three reflections (and as few as none). For another thing, image location varies according to the relative disposition of eye and object. Ptolemy illustrates this point on the basis of figure 7, where the arc represents a section of a great circle on the mirror’s surface, EA a visual ray projected from the eye to A, and AB its reflected ray. O ₁ through O ₆ represent object O at various positions along this reflected ray, and I ₁ through I ₆ the respective images of the object at those positions.

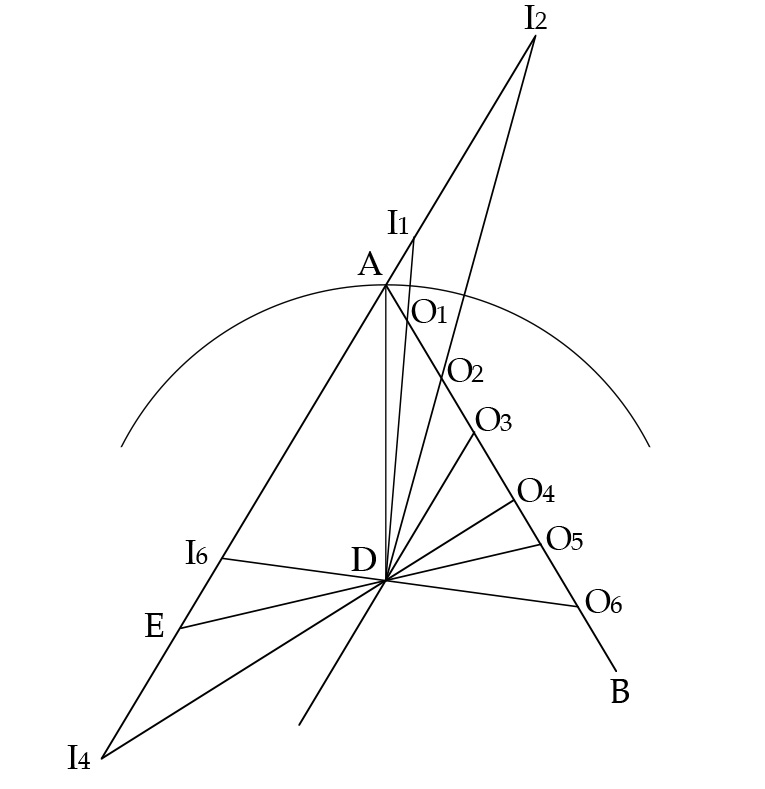
Figure 7: Ptolemy’s diagram for locating images in a concave mirror. Smith, From Sight to Light .

Under these conditions, if the object lies at O ₁ or O ₂ , the respective images will lie at I ₁ and I ₂ , where catheti DO ₁ and DO ₂ intersect the extension of visual ray EA behind the reflecting surface. Thus, as in the case of both plane and convex spherical mirrors, the image will be seen behind the mirror. In this instance, though, as the object moves toward O ₃ , the apparent distance of the image behind the mirror outstrips the actual distance of the object in front of it, and the difference between the two accelerates dramatically until the object reaches O ₃ . Here cathetus DO ₃ and visual ray EA are parallel and thus unable to converge. Without a determinate location at which to see the image, Ptolemy reasons, the visual power forms a nebulous ghost image on the reflecting surface that takes on its shape and color.

Likewise, when the object lies at O ₄ and cathetus DO ₄ intersects the visual ray behind the eye at I ₄ , the image cannot be seen and must therefore be transferred by the visual power to the reflecting surface, where it forms a ghost image. This situation persists as the object moves from O ₄ toward O ₅ , at which point the image location lies in the eye itself. Still unable to see the resulting image, the visual power transfers it to the reflecting surface. However, when the object moves beyond O ₅ , its image becomes directly visible again, as is the case with O ₆ , whose image I ₆ lies between the eye and the reflecting surface. From point O ₆ on, therefore, the image will appear in front of the reflecting surface. ¹²

Wide variations in image displacement are not the only things that set concave mirrors apart according to Ptolemy. Image-size is also quite variable, depending on where the image lies with respect to the reflecting surface. At times, therefore, the image appears much larger than its object, at times the same size, and at times much smaller. In addition, concave mirrors tend to distort the shape of images seen in them, sometimes yielding curved images of plane objects and sometimes yielding plane images of curved objects. Finally, and most salient, concave mirrors will invert images as soon as they are formed between the reflecting surface and the eye. All these points are addressed by Ptolemy in a wide-ranging analysis that far outstrips those of his predecessors in scope and mathematical sophistication.

Ptolemy’s Analysis of Refraction

Ptolemy opens book 5 of the Optics by distinguishing reflection from refraction according to how the visual ray is broken in each case. One way, he contends, “involves rebound and is caused by reflection from bodies that block the [visual ray's] passage and that are included under the heading of ‘mirrors.’” The other way, he continues, “involves penetration and is caused by a deflection in media that do not [completely] block the [visual ray's] passage, and those media are included under the single heading ‘transparent.’” ¹³ Furthermore, he observes, the amount of deflection in refraction varies with the transparent medium that the visual ray penetrates: the greater the density differential between the medium the ray exits and the one it enters, the greater the deflection. That is why visual rays passing from air into glass are bent toward the normal more than those passing from air into water and, conversely, why rays passing from glass into air are bent away from the normal more than those passing from water into air.

In order to determine the amount of such bending, Ptolemy suggests three identically designed experiments to test refraction from air to water, air to glass, and water to glass. We will limit ourselves to the test measuring refraction from air to water because it is simplest. Start with the bronze disk already formed for the reflection experiment, and fashion a semicylindrical vessel just large enough to accommodate it, as represented in cross section in figure 8.

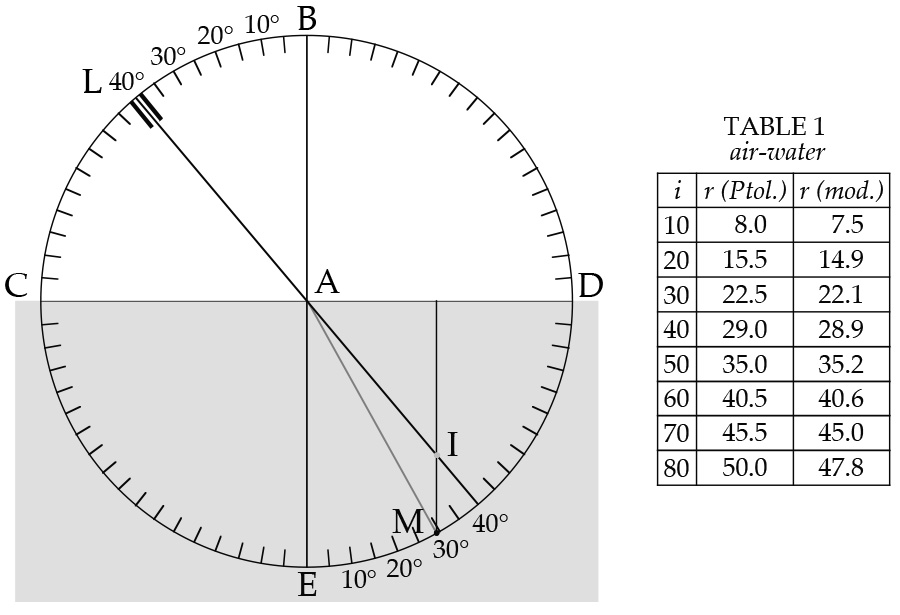
Figure 8: Ptolemy’s experiment for measuring refraction. Smith, From Sight to Light .

After filling the vessel with water, immerse the disk up to its diameter CAD. Align movable arm LA with its sighting device at the 10° mark on arc BC so that angle of incidence LAB for visual ray LA is 10°. Then, peering along line LA, shift the movable arm MA from E toward D until the image of the colored peg at M lines up directly behind the marker at center point A of the disk. According to Ptolemy, the resulting angle of refraction EAM will be 8°. Carry out the same procedure at increments of 10° from 20° to 80° on arc BC, and the resulting angles of refraction will be as listed on table 1. Accordingly, an angle of incidence of 20° will yield an angle of refraction of 15.5°, an angle of incidence of 30° an angle of refraction of 22.5°, and so on.

Two things are noteworthy about this experiment. First, like its counterpart for reflection, it is contingent on the cathetus rule. Thus, when angle of incidence LAB is 40° and the image I of M appears in a direct line along the rectilinear extension of LA, M actually lies below that point at angle of refraction EAM = 29°. Image I is therefore located where the cathetus dropped from M to refracting surface CAD intersects the rectilinear continuation of incident ray LA. Second, the tabulations for the angles of refraction have been adjusted to fit a pattern according to which the angles of refraction decrease incrementally by .5° for every 10° of incidence. Hence, throughout the test, the rate of increase in angles of refraction decreases uniformly at a rate of .5° for every 10°. Perhaps the most striking thing about Ptolemy’s massaged values is how close they are—at least for the most part—to those derived from the modern sine law. And the same applies to his results for refraction from air to glass and water to glass, all of which indicates that he actually conducted the experiments he describes. ¹⁴

After these experiments, Ptolemy takes up the subject of atmospheric refraction in order to demonstrate how celestial observations near the horizon are affected by it. The severity of that effect depends on two things: the density differential between the atmosphere surrounding the earth and the celestial aither outside it, and the height of the atmospheric shell. Since neither is known with any certainty, Ptolemy concludes, we cannot determine the actual amount by which atmospheric refraction skews celestial observation. We can, however, be certain that this skew is greatest at or near the horizon and least at zenith. ¹⁵

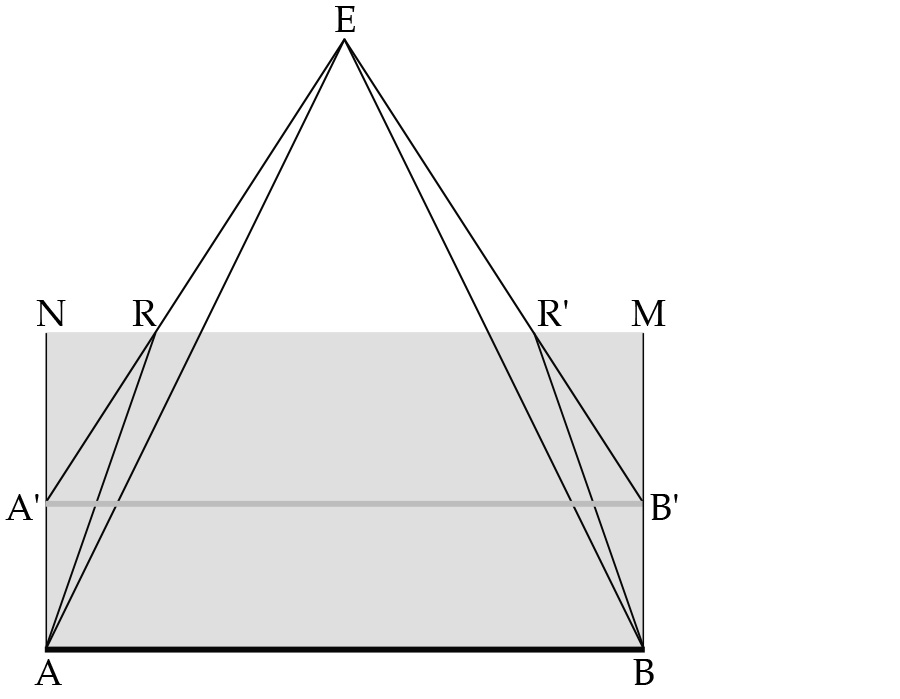
Figure 9: Refraction causes an object submerged underwater to appear closer than it actually is. Smith, From Sight to Light .

Ptolemy goes on to discuss how image location and image size are affected by the refraction of visual rays passing from air into water through plane, convex, and concave interfaces. The simplest case involves passage through plane interfaces. Assume, for instance, that AB in figure 9 is an object immersed in water below surface NM, and let E be an eye looking down at it. If there were no water in the way, then the eye at E would see endpoints A and B of the object, and thus the object as a whole, under visual angle AEB. However, when the eye looks at the object through refracting surface NM, it will see the images of endpoints A and B at A’ and B’, where catheti AM and BM intersect visual rays ER and ER’ extended below surface NM. AB will therefore be seen under visual angle A’EB’, which is larger than visual AEB, so it will appear magnified. In addition, since A’B’ is higher than AB, it will appear closer than it actually is. ¹⁶

Ptolemy’s study of refraction in book 5 stops jarringly in the middle of an analysis of image distortion when an object in a denser medium is viewed through a convex surface. Where his overall analysis might have gone from there is anyone’s guess. Still, incomplete though it is, Ptolemy’s Optics represents the ne plus ultra of classical optics, and, as will become clear in due course, it provided the analytic foundations for optics over the next fourteen centuries, much as his Almagest did for astronomy—although in a more indirect and oblique way. Particularly significant in this regard was his threefold distinction among unimpeded, reflected, and refracted vision.

The Anatomy and Physiology of the Visual System

For the canonical account of ocular anatomy and physiology during the classical period, and indeed well into the late Renaissance, we look to Ptolemy’s much younger contemporary, Galen. According to him, the visual system originates in the brain and the two integuments encasing it: the tough, outer dura mater, and the softer pia mater beneath it. Inside the brain are four interconnected cavities or ventricles, a paired anterior set connected to a central ventricle that is in turn connected to an occipital ventricle. From the front of the paired anterior ventricles the two hollow optic nerves emerge, each protected by an outer sheath of dura mater and an inner one of pia mater. Soon after emerging, the two nerves join at the optic chiasma and then part to enter the eye sockets, where they bulge out to form the two eyes and their encasing tunics. At the front of the eye, protected by the transparent cornea and the iris, lies the oblate crystalline lens.

Physiologically, this entire system of ventricles and hollow nerves is infused with pneuma distilled from arterial blood at the base of the brain. Forming the material substrate for our sensitive, perceptual, and intellectual capacities, this subtle fluid flows continually from the brain through the hollow optic nerves and eyes to each crystalline lens. From there it reaches into the sunlit outer air, which it transforms into a percipient extension of the eye, thereby establishing visual contact with external objects. It also endows each lens with the visual sensitivity that enables it to apprehend the color-based representations of those objects conveyed back through the pneumatized air. Each eye sees things from a slightly different perspective, though, so the two eyes apprehend slightly different representations of the same thing. Transmitted through the optic nerves to the optic chiasma, where the two nerves join, these two representations are fused into a single, common representation that is then remanded to the brain for further perceptual and intellectual processing. Diplopia results from the failure of such fusion. ¹⁷

With this model of the visual system Galen provided a framework for mapping the visual process according to stages of apprehension, starting with mere sensation at the crystalline lens, advancing to perception at the front of the brain, and culminating with cognition in the brain’s central and occipital ventricles. As we will see eventually, this mapping process was brought to completion during the Middle Ages and resulted in a sophisticated model of vision that explained not only how we see external reality but also, and more important, how we picture it in our minds.

The Ancient Study of Burning Mirrors

To this point the focus of analysis has been on visual rays, not light rays. When light entered the analysis at all, it did so as a precondition or catalyst for sight, not as a subject of study in its own right. This applies equally to Plato, Aristotle, Ptolemy, and Galen, all of whom specify color, not light, as the primary object of vision. It also applies to Euclid and Hero, who ignore light almost entirely. As a rule, therefore, light and its physical manifestations were of secondary interest to ancient optical theorists. One idiosyncratic breach of this rule is found in the study of burning mirrors and their focusing properties, although here it is not so much light as the heat associated with it that is at issue.

An early effort to explain such mirrors comes in the last proposition of Euclid’s Catoptrics . There Euclid offers a specious geometrical explanation of the focusing property of concave spherical mirrors. If such mirrors face the sun directly, he contends, then they will reflect all the solar rays that pass through their center of curvature back to that center point, where enough rays will converge to cause burning. In short, the center of curvature represents the point where enough sunlight is concentrated to generate significant heat. ¹⁸

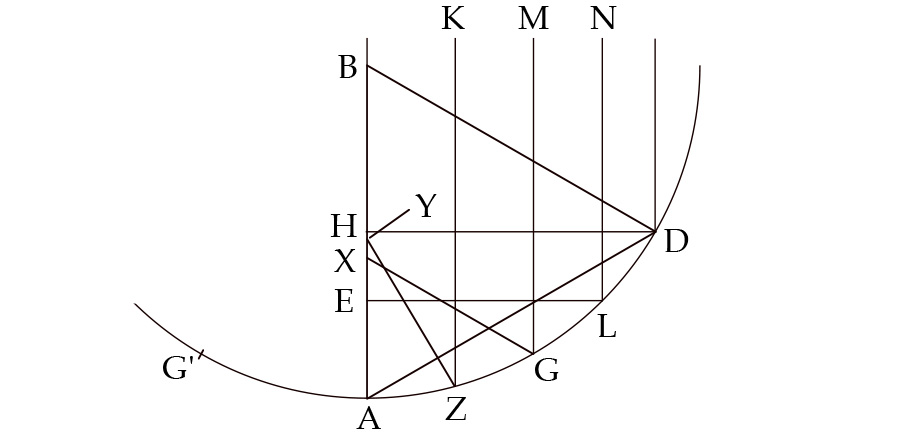
Figure 10: Diocles’s demonstration of the focal point of a spherical concave mirror. Smith, From Sight to Light .

Within roughly a century, this botched conclusion was corrected in Diocles’s On Burning Mirrors (c. 200 BCE). Contrary to Euclid, Diocles demonstrated conclusively that the focal point of a spherical concave mirror is not at its center of curvature but at half the radius of curvature above the surface along its axis. The proof is simplicity itself. Let arc G’AD in figure 10 be a cross section of the surface of a concave spherical mirror whose center of curvature is B, let radius BA be on its axis, and let KZ, MG, and NL be solar rays parallel to that axis. Let H bisect radius BA. On this basis Diocles shows that, as the rays strike the mirror’s surface ever closer to point A, their reflected rays strike ever closer to H on axis AB but never quite reach it. More important, however, he shows that the maximum concentration of rays intersecting along AB occurs in a tiny area just below H, not at an actual point, and it is here that the concentration is great enough to cause burning.

Figure 11: Parallel rays striking a parabolic mirror will converge at focal point F. Smith, From Sight to Light .

Whereas spherical concave mirrors bring light to a focal area, paraboloidal mirrors bring it to an actual point. Diocles demonstrates this fact on the basis of figure 11, where MBK represents a cross section of a paraboloidal mirror with axis BZ’ on which F is the focus. Pick random point Q on surface MBK and draw AQ tangent to it. Then erect a perpendicular at Q and extend it until it intersects the axis at Z. Diocles goes on to prove that solar ray SQ parallel to axis BZ’ and forming angle of incidence SQZ will reflect to F at equal angle FQZ. The same holds for any other solar ray, such as S’Q’, so all solar rays reaching the mirror along rays parallel to axis BF will reflect to F. Since they converge at an actual point and are thus perfectly focused there, they will generate as much heat as possible—far more than at the focal area of a concave spherical mirror. ¹⁹

From Greek to Arabic: 200 CE to 1100 CE

Interest in geometrical optics seems to have dwindled markedly by the third century CE. An indication of this decline is that, as far as we can tell, Ptolemy’s Optics went virtually unread throughout late antiquity and into the early Middle Ages. Furthermore, the few texts from that period that do deal with geometrical optics reveal either a rudimentary understanding or, worse, a misunderstanding of ray analysis and its principles. There were a few bright spots. One was Anthemius of Tralles’s early sixth-century discussion of burning mirrors in “On Mechanical Wonders” ( Περί παραδόξων μηχανημάτων ). Among the more interesting things he shows in that work is that if sunlight is funneled onto an ellipsoidal mirror through one of its two foci, all the reflected light will converge at the other focus and thus be brought to a point of intense heat. He also demonstrates the focusing property of paraboloidal mirrors in a more elegant way than Diocles by basing his proof on the focus-directrix property of the parabola. ²⁰

There were cultural factors behind this apparent decline. For one thing, the third-century split of the Roman Empire into Greek East and Latin West, coupled with the Germanic incursions into the latter portion, left it culturally and intellectually stranded. Whereas facility in Greek had been common among the educated elite of the early Roman empire throughout, it became increasingly rare in the Latin West from the fourth century on. Consequently, the intelligentsia of the Latin West lost direct contact with the classical Greek tradition of philosophy, science, medicine, and mathematics. What little contact they did have came through a meager stock of Latin translations, such as Calcidius’s fourth-century translation of Plato’s Timaeus . As a result, western thinkers knew tantalizing bits about that tradition at second hand with virtually no real understanding of its textual sources.

The Greek East had its own share of problems. Riven by bitter religious disputes from the fourth century on, it faced an active and implacable enemy in the Persian empire, which it eventually defeated in a Pyrrhic victory that opened the way for a successful invasion by Muslim Arab forces in the second half of the seventh century. Amid all this turmoil there was continuing interest in classical Greek philosophy among a small, but influential group of Neoplatonist thinkers, who attempted to reconcile Plato and Aristotle by papering over the apparent differences between them. This process resulted in a somewhat Platonized version of Aristotle’s thought about sense perception as a multi-stage process leading to cognition, all within the ventricular system of the brain.

From Greek into Arabic

On the face of it, the establishment of Arabic dominance over the Middle Eastern and North African reaches of the Roman Empire did not bode well for intellectual development in that area. Yet, during the Abbasid Caliphate, which acceded in 750 and took Baghdad for its capital, growing interest in foreign scientific and philosophical texts impelled high-level patrons to commission translations of them. Consequently, by the end of the ninth century a sizeable compendium of Greek works had been rendered into Arabic, and it was augmented significantly during the tenth century. Arabic thinkers of all stripes now had direct access to a vast trove of Aristotelian writings, along with numerous Neoplatonic commentaries. They also had a wide range of scientific and mathematical works at hand, including an extensive array of Galen’s writings. In short, they were now privy to the most advanced Greek thought in philosophy, medicine, mathematics, technology, and science. ²¹

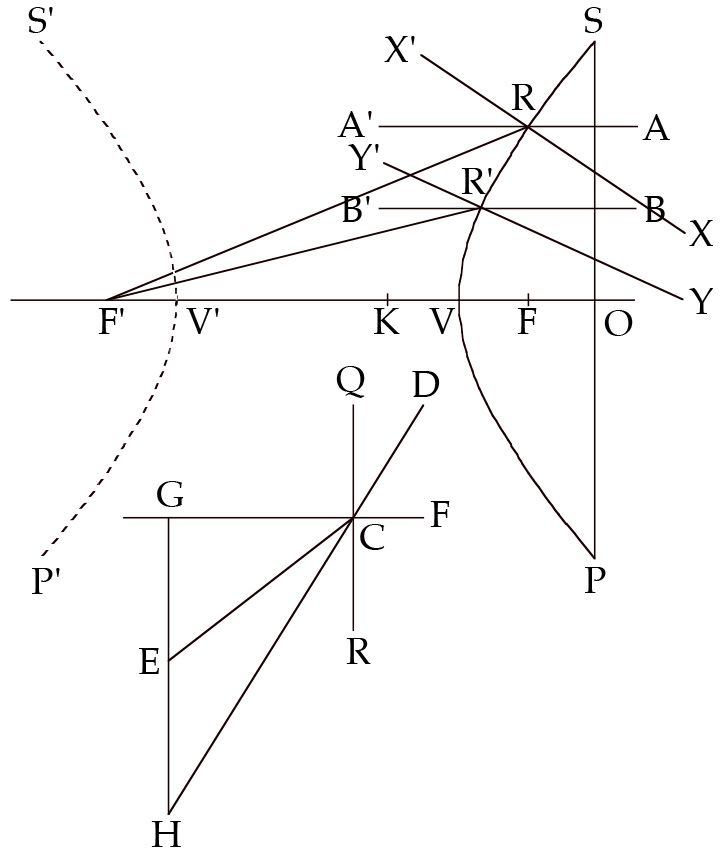
Figure 12: Ibn Sahl’s demonstration of the focal point F’ of a plano-hyperbolic lens. Smith, From Sight to Light .

Arabic thinkers did not just sit on this bequest. They elaborated on it in innovative and often ingenious ways. A prime example of such elaboration is On Burning Instruments by the late tenth-century Baghdadi mathematician Ibn Sahl. Two things set this work apart. First, in addition to addressing the standard selection of burning mirrors (spherical, ellipsoidal, and parabolic), Ibn Sahl includes a discussion of lenses. Second, in that discussion he deals with plano-hyperbolic lenses. Briefly, what he shows is that parallel solar rays entering the plane surface of such lenses—for instance, AR and BR’ in figure 12—will be brought to perfect convergence at focus F’ of the facing branch of the hyperbola. More to the point, however, the construction for the proof depends on a constant ratio between CH and CE in the ancillary diagram, which amounts to a permutation of the sine law of refraction commonly credited to Willibrord Snel (d. 1626). ²²

Ibn Sīnā (d. 1037), or Avicenna as he was known in the Latin West, provides another example. Widely read, he was especially knowledgeable about Aristotelian philosophy and Galenic medical thought, both of which figure prominently in his account of visual perception and its basis in the psychology of distinct faculties, or “internal senses.” Not surprisingly, given his Aristotelian leanings, Avicenna favored intromissionism. However, he differed with Aristotle over light and its function in the visual process. Aristotle, as mentioned earlier, supposed that light transforms the continuous aerial medium between object and eye from potentially to actually transparent, thereby allowing the object’s color to be seen through it. Avicenna, on the other hand, gave light a more direct role according to its innate capacity to radiate through transparent media. If it encounters an opaque object, it illuminates the color on its surface, thus rendering it visible and empowering it to radiate through the transparent medium to our eyes.

Following Galen, Avicenna locates the seat of vision in the crystalline lenses, which are sensitized by visual spirit (a form of Galenic pneuma) flowing into them from the brain through the hollow optic nerves. The luminous color striking the sensitized lenses forms a visual impression on each that is then conveyed through the hollow optic nerve to the optic chiasm, where the two visual impressions are fused and then sent onward to the paired anterior ventricles of the brain. There they are remanded to the common sense, which forms an abstract, composite representation of the object according not only to its visible qualities but also to its other sensible qualities. Known in later Latin scholastic parlance as sensible species, such abstract representations are then passed to the imagination, which serves as a short-term memory of sorts.

These abstract representations can be thought of by analogy to images insofar as, like images, they somehow convey what the object is without being the object itself. Think, for example, of a painted portrait, which is nothing more than a concatenation of colors on a flat surface. Nonetheless, the way these colors are juxtaposed provides clues about such things as size, shape, depth, and so forth that enable us to recognize not only that the portrait represents a person but even who it represents. Such clues constitute what Avicenna, and many of his Arabic compeers, refer to as intentions, and it is through apprehending them that the common sense makes perceptible sense of the visual representations passed to it from the crystalline lens. Like images, therefore, these abstract representations are intentional likenesses of the objects they represent.

These likenesses represent objects in all their physical particularity, but, like the particular sense impressions that give rise to them, they bear certain intentions that express their meaning at a more general, abstract level. It is at this level that the reasoning faculty in the middle ventricle operates, apprehending the intentions borne by the particular sensible representations and abstracting general representations from them. This is how reason moves beyond a perceptual grasp of particular things to an intellectual understanding of what kinds of things they are at the most general level. The representations that such understanding yields are referred to by subsequent Latin scholastics as intelligible species. On their basis we form a faithful mental picture of external reality and its deep taxonomic structure —provided, of course, that our sensitive, perceptual, and intellectual faculties function properly according to their natural capacities. ²³

Avicenna did not create this model of perception and cognition ex nihilo . He worked within a tradition of analysis and interpretation that had evolved steadily during late antiquity and was passed down to such Arabic philosophical luminaries as Yaʿqūb al-Kindī (d. 873) and Abū Naṣr al-Fārābī (d. 950). Avicenna’s model was therefore a particular—and, as it turns out—particularly influential elaboration within that tradition. The same holds to some extent for Ibn Sahl, whose work on burning instruments clearly builds on the tradition of Diocles and Anthemius of Tralles, although he extends his analysis beyond reflection to refraction. As far as visual analysis is concerned, he had such ninth-century predecessors as al-Kindī, Qusṭā ibn Lūqā, and Aḥmad ibn ʿĪsā, but what sets him definitively apart is that, unlike them, he had access to Ptolemy’s Optics in Arabic translation. As far as we know, he was the very first to have had such access.

Ibn al-Haytham and the Culmination of Arabic Optics

A close contemporary of Avicenna, Ibn al-Haytham (d. 1040/41) shared the same basic understanding of sensation, perception, and cognition according to distinct stages linked to distinct psychological faculties. In short, he fell within the same tradition of analysis and interpretation. Unlike Avicenna, however, he was an extraordinarily gifted mathematician, and he brought that gift to bear with elegant precision in his monumental Kitāb al-Manāẓir (“Book of Optics”). Composed in the 1030s, this work offers an exquisitely systematic and detailed account of visual perception according to whether visual contact is direct and unbroken, completely broken by reflection, or partially broken by refraction. In short, Ibn al-Haytham followed the same order of analysis as Ptolemy did in his Optics . This is no accident. Ibn al-Haytham was thoroughly familiar with Ptolemy’s Optics and used it as a guide for his own analysis of vision. To a great extent, in fact, the Kitāb al-Manāẓir represents both a thorough revision of, and a grand elaboration on Ptolemy’s Optics .

A crucial point of difference between Ibn al-Haytham and Ptolemy involves the direction of radiation and, therefore what is radiated. For Ptolemy it was visual rays. For Ibn al-Haytham it was light. Light, he argued, is a particular quality of luminous or illuminated bodies that radiates in all possible directions through transparent media. Specifically, each point on the surface of such bodies forms a sphere of radiation through the surrounding transparent medium, and each such sphere can be thought to comprise a virtual infinitude of rays emanating from the center. In reality, though, light emanates from tiny spots, not points, on the luminous surface, so the sphere of radiation actually consists of infinitesimally thin cones, not geometrical lines, extending from its central spot. Like Ptolemy, therefore, Ibn al-Haytham conceived of the mathematical ray as an imaginary analytic device, albeit an extraordinarily useful one. ²⁴

Figure 13: Ibn al-Haytham’s model of the human eye. Smith, From Sight to Light .

According to Ibn al-Haytham, radiated light manifests itself physically by illuminating opaque objects and, in the process, rendering the color of their surfaces luminous. In that state the color is able to radiate spherically from every spot on those surfaces, and when it reaches a properly receptive eye, it is seen. How it is seen is determined by the visual system’s anatomical and physiological structure. Anatomically, the eye as conceived by Ibn al-Haytham is illustrated in figure 13, which shows it in cross section. The essential features are: 1) the outer enclosing scleral sphere centered on C, its front portion constituting the transparent cornea; 2) the inner uveal sphere with its pupillary aperture in front and its center ahead of C on the visual axis; 3) the biconvex lens inside the uveal sphere, its front surface concentric with the outer, scleral sphere. The basin between the cornea and the front of the lens is filled with a thin fluid called albugineous humor, the lens with a more refractive fluid called glacial humor, and the rest of the eye behind the lens with an even more refractive fluid called vitreous humor. Finally, at the very back of the eye is the hollow optic nerve which serves as the conduit for visual spirit flowing from the brain to the lens, thus rendering it visually sensitive. ²⁵

Assume that AB is an object facing the eye, and let the luminous color from endpoint A radiate spherically in all directions. Of all the rays projected from A to the eye, only one strikes the cornea and the front surface of the lens along the orthogonal to pass toward center point C. The rest are refracted out of the way, as is the ray refracted toward point D inside the eye. The same applies to all the rest of the points on object AB; only one ray from each point will pass orthogonally through the cornea and front surface of the lens toward C. All such rays will form a cone of radiation circumscribed by the pupil, its base defining the field of view and its vertex at the very center of the eye.

Striking the front surface of the lens directly, each of these rays makes an impression on it that is visually sensed. The totality of all these sensed impressions forms a sort of pointillist image of the objective source according to the juxtaposition of colors. This image is then passed in proper order, spot by spot and ray by ray, to the posterior surface of the lens. There the rays are refracted into the vitreous humor at just the right angles to be shunted into the hollow optic nerve while maintaining their proper order. That same order is rigidly maintained as the images from both eyes wend their way to the optic chiasma. After fusion, the amalgamated image is conveyed to the brain for perceptual adjudication. ²⁶

According to Ibn al-Haytham, this adjudication is based on what he calls visible intentions. Altogether there are twenty-two of them, and aside from light and color, which are per se visible, they include such things as size, shape, distance, motion, rest, and even beauty and ugliness. Some or all of them are “in” the pointillist visual image elicited by the lens in much the same way that key defining features are “in” a painted portrait according to shadings and color contrasts. Like the subject of a portrait, therefore, what the visual image represents must be realized through inference. Carried out by the so-called faculty of discrimination, this realization involves a careful visual scanning of the given object and concomitant judgments of its implied characteristics, all by reference to the vertex of the cone of radiation. The so-called center of sight, this constitutes the viewpoint from which everything is visually judged. When properly done, the process of visual discrimination yields what Ibn al-Haytham calls a “particular form,” which represents the object in all its physical specificity and is retained in the imagination.

Armed with a store of such particular forms, we are able to compare new ones to them in order to find a proper match. Repeated comparisons of this sort that yield exact or close matches provide a more general apprehension of the types of things the particular forms represent. That apprehension in turn gives rise to the so-called universal form. An example of the passage from particular to universal form would follow from the eventual recognition that this particular schnauzer, that particular cocker spaniel, and that particular doberman pinscher are all dogs. It is therefore through the acquisition of universal forms that we taxonomize external reality and in so doing form an overarching world view. ²⁷

Like Ptolemy, Ibn al-Haytham assumed that under the right conditions visual perception is veridical. Misperception occurs when the conditions are less than optimal. Perhaps the light is too dim, the object too far away, the eyesight too compromised, the glance too passing, the air too smoky; all of these shortcomings can cause the visual faculty to misperceive. So too, if the two eyes do not align their axes properly on an object, they may see it double. Perhaps the most interesting misperception Ibn al-Haytham deals with is the moon illusion, according to which the moon and sun often look much larger at the horizon than at zenith, even though they are actually the same size at both places.

Ibn al-Haytham’s explanation is that we perceive the sky as a ceiling rather than as a dome, so as the moon passes from zenith to horizon, it looks as though it is receding ever farther away along the heavenly ceiling. Since it subtends the same visual angle throughout, however, we perceive it as larger according to its increased distance. Underlying this explanation is Ibn al-Haytham’s acceptance of the size-distance invariance hypothesis, according to which a given object always looks the same size as it recedes from us even though it is seen under a continually decreasing visual angle. Conversely, if it is seen under the same visual angle as it recedes from us, it will look larger. On that basis, Ibn al-Haytham rejected Ptolemy’s geometrical explanation of why objects appear magnified when seen underwater insofar as the increase in visual angle is offset by the apparent approach of the object. ²⁸

Ibn al-Haytham on Reflection

As we saw earlier, Ptolemy relied on experiments to confirm certain optical principles. Ibn al-Haytham did too, but on a much more consistent basis than Ptolemy. Early in the Kitāb al-Manāẓir, for instance, he takes great pains to show empirically that the eye sees by reception of light and luminous color rather than by its own agency—in short, that sight depends entirely on intromission. He also suggests a variety of simple experiments to prove that light and luminous color radiate in straight lines.

Figure 14: Ibn al-Haytham’s demonstration of the law of equal angles. Smith, From Sight to Light .

Ibn al-Haytham’s experimentalism reached its highest level of sophistication in confirming the equal angles law of reflection on the basis of seven representative mirrors: plane; convex spherical, cylindrical, and conical; and concave spherical, cylindrical, and conical. The apparatus he designed to that end is illustrated in figure 14, as viewed from directly above. It consists of a hollow wooden cylinder around five inches high with an outer diameter of slightly more than 10 inches and an inner diameter of around 7.5 inches. At a level 1.5 inches above the cylinder’s base, it is pierced with a narrow opening at A pointing directly at centerpoint V. On the right-hand side of A narrow openings pointing directly at V are bored at B, C, and D, and on the opposite side openings at B’, C’, and D’ are drilled equivalently so that angles AVB, AVC, and AVD are equal respectively to angles AVB’, AVC’, and AVD’.

Next, the seven representative mirrors are fashioned from highly polished iron, and each of them is placed in turn against point V so that AV is perpendicular to its surface. When things are properly set up for each mirror, sunlight is allowed to stream through the narrow opening at B toward V while all the other openings are blocked. In that case, the light radiating along BV will reflect from the mirror along B’V at the same angle and will form a bright spot on the inner surface of the cylinder right where B’V meets it. Likewise, when the openings at C and then D are exposed while the others are blocked, their light reflected from V will cast a bright spot where VC’ and VD’ intersect the inner surface of the cylinder. It therefore follows not only that the light reflects at equal angles but also that all the reflections occur in a single plane. ²⁹

The difference between this and Ptolemy’s experimental verification of the equal angles law comes to ground in the difference in what was being measured. For Ptolemy it was the reflection of visual rays. For Ibn al-Haytham it was the reflection of light rays. Consequently, he had to revise the experiment so that the light, or at least its physical effect, could be seen directly rather than indirectly, as was the case in Ptolemy’s experiment. That is why the reflections are confined in the darkened hollow of the cylinder, so that at least the spot cast by reflection is clearly visible, although if the air in the hollow is even slightly misty or dusty, the actual beams of incident and reflected light are visible. Unlike Ptolemy, therefore, Ibn al-Haytham faced experimental constraints that forced him to design a more complex apparatus that was nonetheless more limited in its application than Ptolemy’s.

Having shown how to confirm the equal angles law experimentally, Ibn al-Haytham turned to an experimental verification of the cathetus rule. The verification itself involves posing a thin rod upright on the mirror’s surface and determining that its image (or a small portion of its image in the concave mirrors) lies directly in line with it below that surface along the perpendicular. More to the point, if we conceive of the rod as composed of individual spots, then we can see that the image of each spot lies directly in line with it below the surface along the perpendicular. We can also see that the spot’s image appears along a direct line of sight through that surface. Reducing the phenomenon to individual spots therefore universalizes the cathetus rule for any spot on any object viewed in a mirror. ³⁰

With the rules for determining image location empirically verified, Ibn al-Haytham takes up their application in all seven representative mirrors, starting with point objects and then moving on to extended objects. On the whole, his analysis offers little beyond what Ptolemy had already established in the Optics , although Ibn al-Haytham’s account is far more sophisticated mathematically than Ptolemy’s. A case in point is his set of solutions to what later became known as “Alhazen’s Problem,” which was formulated as follows by Christiaan Huygens in 1669: “Given a concave or convex [spherical] mirror and given an eye and a point on a visible object [facing it], to find the point [or points] of reflection.”

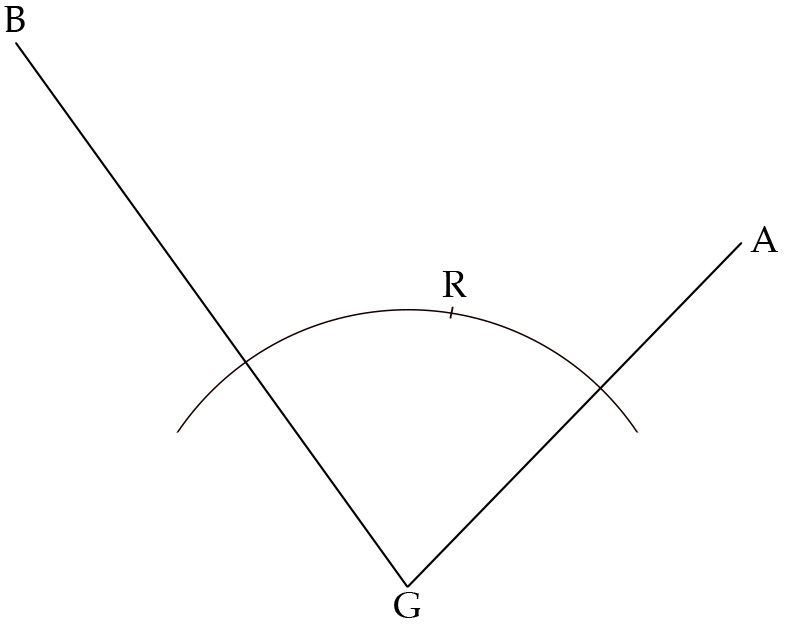
Figure 15: Set-up to Ibn al-Haytham’s demonstration of the point of reflection on a convex spherical mirror. Smith, From Sight to Light .

Whereas Huygens gave a single, general solution that covered all possibilities at once, Ibn al-Haytham approached the problem piecemeal according to cases, the first of which involves the convex spherical mirror from which only one reflection is possible. The problem here is straightforward enough. Let the arc in figure 15 be a segment of a great circle on the reflecting surface with center of curvature G. Let B be a point of radiation and A the center of the eye, and let AG ≠ BG. The problem is to find point R on the arc within angle BGA. Simple enough on its face, this problem is quite complex. In order to solve it, Ibn al-Haytham had to provide six ancillary proofs before even turning to the main solution, which depended in part on a knowledge of conic sections.

As regards concave spherical mirrors, Ptolemy had shown that there could be as many as three reflections, and Ibn al-Haytham added that, if the eye and point of radiation were enclosed within the sphere, there could be as many as four. He therefore set himself the problem of determining precisely where the point of reflection was for each of them.

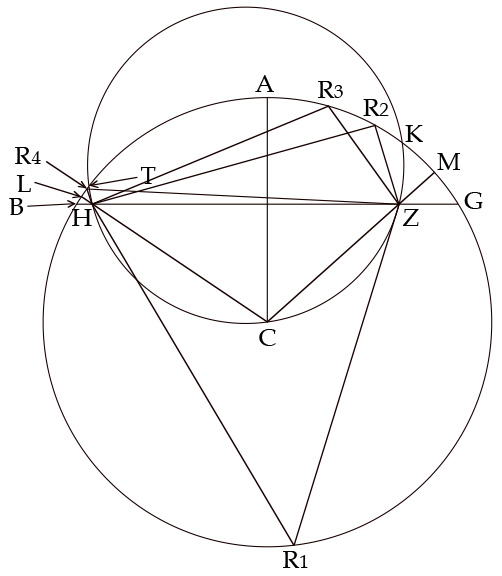
Figure 16: Ibn al-Haytham’s demonstration of the points of reflection on a concave spherical mirror. Smith, From Sight to Light .

The conditions of the problem are illustrated in figure 16, where the large circle BAG with center of curvature C represents the section of a great circle through the mirror. Chord BG lies above C, and perpendicular AC is drawn through it. H and Z on chord BG represent a point of light radiation and a center of sight, respectively, and they lie at unequal distances from the intersection of chord BG with AC.

As Ptolemy had already demonstrated, if a circle is drawn through H, C, and Z so that it extends beyond A and intersects the mirror at T and K, then two reflections will occur on the arc between A and K, and one reflection will occur between H and T on arc AB. In addition, one reflection will occur on arc BG below C. Within this context, the problem facing Ibn al-Haytham was to find a method for locating points of reflection R ₁ –R ₄ . His solution was to pinpoint each in that order. As with the convex mirror, the method, which was tailored to each case, was conceptually simple but technically complex, far too complex to detain us here. ³¹

Ibn al-Haytham on Refraction

Just as Ibn al-Haytham followed Ptolemy’s lead in confirming the equal angles law of refraction, he did so in testing refraction from air to water, air to glass, and glass to water. And just as before, he redesigned the experimental apparatus to test light rays rather than visual rays. Accordingly, we are to construct the panlike device illustrated in figure 17, starting with a bronze disk roughly 20” in diameter to form the base, which we divide into quarters by diameters FG and DE passing through center point C.

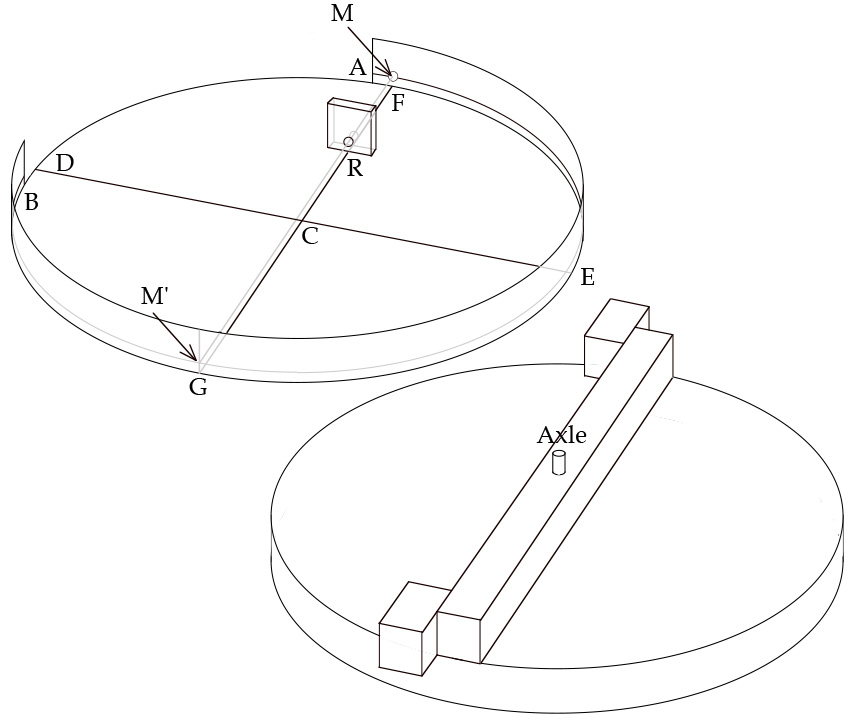
Figure 17: Ibn al-Haytham’s apparatus for measuring light refraction. Smith, From Sight to Light .

We then attach a partial rim 1.5” high to its perimeter extending from A to E and draw a line on the inside of the rim’s surface at a height of .33 inches. At point M on that line, just above F, we drill a hole .33 inches in diameter. Then we form a small square panel, drill a hole .33 inches in diameter in it at the same height as the hole at M, and attach it to the pan at R on radius FC. An imaginary line from M through the center of the hole in the square panel will therefore pass along and just above FG to point M’ right above G on the other side of the pan. Starting from M as the zero point, we divide the line on the inside of the pan’s rim, which passes through M’ to B, into degrees and fractions of degrees as feasible. Finally, we affix an axle to the back of the pan at its center and slip a hanging strip onto it, as pictured in the bottom diagram of figure 17. That done, we suspend the apparatus by its hanging strip in a vessel just large enough to accommodate it, as illustrated in figure 18. So disposed, the pan can be rotated freely on its axis.

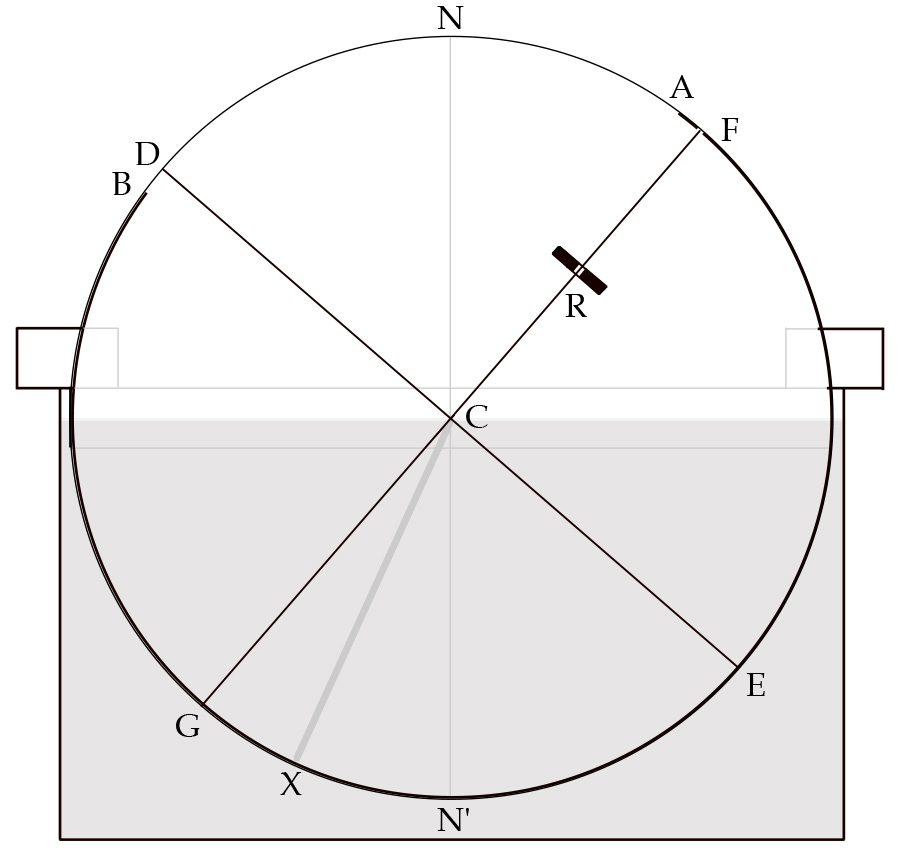
Figure 18: The apparatus from figure 17, using sunlight to measure the angle of refraction as light passes from air to water. Smith, From Sight to Light .

As before with Ptolemy, we will confine ourselves to the simplest test, which involves refraction from air to water. First, we place the entire contrivance, pan and holding vessel, toward the sun, fill the holding vessel with water up to the level of C, and rotate the pan counterclockwise until diameter FG reaches a predetermined angle FCN with respect to normal NCN’. That angle will be the angle of incidence, and ideally it should be initially set at 10°. When the sun reaches the right height to form such an angle, it will project a thin beam of sunlight straight through the holes at F and R along diameter FG. On reaching C, the beam will be broken at the water’s surface and, instead of passing straight through to G, it will be diverted to X, where it will form a bright spot. Angle XCN’ will therefore be the angle of refraction. To complete the test, we simply repeat the process for angles of incidence between 10° and 80°. The same basic procedure can be followed for air to glass and glass to water.

Given the precision and detail of Ibn al-Haytham’s description of the apparatus and its application, we would expect the resulting tabulations to have been at least as accurate as, and most likely more accurate than, those given by Ptolemy. Not only is that not the case, but, surprisingly enough, Ibn al-Haytham provides no tabulations at all. This failure, coupled with other problematic aspects of the refraction experiments suggest that he never actually conducted those experiments as described but, rather, presented them as carefully contrived thought experiments. Equally questionable is that he conducted the reflection experiment as described because of the exceptional precision required of the apparatus, precision beyond the technology of his day. ³²

From these experiments, putative or real, Ibn al-Haytham draws some conclusions. One is that refraction occurs in a single plane perpendicular to the refracting interface. Another is that when refraction occurs from a rarer to a denser medium, the angle of incidence is always greater than the angle of refraction, and the opposite holds for refraction from a denser to a rarer medium. In both cases, however, the angles of incidence and refraction approach equality as the angle of incidence approaches 0°. Also, refraction is perfectly reciprocal, so that the path followed by light in refracting from a rarer to a denser medium will be precisely the same if the direction of radiation is reversed.

Ibn al-Haytham then turns to an empirical verification of the cathetus rule of image location for refraction in anticipation of a fairly lengthy analysis of atmospheric refraction and its effect on celestial observation. This analysis culminates in the demonstration that, although atmospheric refraction at the horizon can magnify objects by a miniscule amount, such magnification is not enough to explain the moon illusion, which can only be accounted for on the psychological grounds discussed earlier: namely, according to our perception of the sky as a plane parallel to the plane of the horizon.

Capping his treatment of refraction, Ibn al-Haytham’s psychological explanation of the moon illusion brings his Kitāb al-Manāẓir to a somewhat abrupt close. The parallel here with Ptolemy’s Optics is obvious but accidental: there is no reason to suppose that, unlike the Optics , the extant version of the Kitāb al-Manāẓir is incomplete. Still, there are enough real parallels between the two works to warrant the conclusion that, rather than undermining Ptolemy’s optical analysis, Ibn al-Haytham brought it to a perfection of sorts. A clear example lies in his solution of “Alhazen’s Problem,” which completed a study of concave spherical mirrors left tantalizingly unfinished by Ptolemy.

There is another telling parallel between the two works. Like Ptolemy’s Optics , Ibn al-Haytham’s Kitāb al-Manāẓir appears to have made little or no immediate impact within its own cultural sphere, although it did find a perceptive critic in Kamāl al-Dīn al-Fārisī, whose early fourteenth-century Tanqīḥ al-Manāẓir (“Revision [of Ibn al-Haytham’s] Optics”) represented a significant step forward (we will return to him later). But Kamāl al-Dīn al-Fārisī seems to have been the exception. For the most part, Ibn al-Haytham’s Kitāb al-Manāẓir was all but ignored within its own cultural and linguistic context yet, like Ptolemy’s Optics , found a dynamic future in translation, this time from Arabic to Latin.

From Arabic to Latin: 1100-1500

While Arabic thinkers were coming into their own during the ninth, tenth, and eleventh centuries, primarily on the basis of newly recovered Greek work, the Latin West was still textually adrift from the classical Greek past. Acutely aware of this shortcoming, western intellectuals were eager to gain access to the original texts. The opportunity came in the twelfth century as Christian powers gained control of Muslim territory in the Iberian Peninsula and Sicily. Emblematic of this power shift was the capture of Toledo in 1085 and with it the sudden acquisition of libraries containing a wealth of Arabic texts, including not only Greek philosophical and scientific texts, but also elaborations on them by the likes of al-Kindī, al-Fārābī, and Ibn Sīnā.

Attracted by this new opportunity, northern scholars soon found their way to the Iberian Peninsula either to commission translations or carry them out on their own. Thus, by the end of the twelfth century, a significant body of Greek works and Arabic had been rendered into Latin, and considerably more was added to it during the first three quarters of the thirteenth century. Key for our purposes is that these translated works included Avicenna’s Canon and Shifa (“Book of Healing”), the optical treatises of Euclid, Hero, and Ptolemy, and—most important of all—Ibn al-Haytham’s Kitāb al-Manāẓir , which was rendered into Latin as De aspectibus (“On Visual Appearances”) and attributed to Alhacen, the Latin transliteration of Ibn al-Haytham’s given name, “al-Hasan.”

The Perspectivist Optical Tradition

One of the earliest western thinkers to study geometrical optics seriously after the recovery of its Greek sources was Robert Grosseteste (d. 1253), who wrote several brief optical tracts. Among these, De lineis, angulis, et figuris (“On Lines, Angles, and Shapes”) is especially noteworthy for the broad claim that “a consideration of lines, angles, and figures is of the greatest utility because it is impossible to gain a knowledge of natural philosophy without them.” ³³ Although in fact Grosseteste’s application of this principle to optics was not always felicitous, his confidence in geometry as the key to understanding light and sight was shared by a small group of subsequent thinkers, who had access to a much richer stock of optical sources, Alhacen’s De aspectibus foremost among them. Consisting of Roger Bacon (d. 1292), Witelo (d. 1280?), and John Pecham (d. 1292), this group laid the foundations for the science of geometrical optics (Latin perspectiva ) in the medieval Latin West. In doing so they brought Alhacen into the mainstream of medieval and Renaissance optical thought.

Inspired by Grosseteste, Roger Bacon was the earliest and perhaps most eclectic of these three thinkers. Forming part 5 of his Opus majus , which he sent to Pope Clement VII in 1267, his major study of optics was later excerpted as an independent treatise under the title Perspectiva and circulated quite widely as such. Although Bacon relied most heavily on Alhacen for theoretical principles, he drew freely upon the optical works of Euclid, Ptolemy, and al-Kindī for elaboration and examples. He also simplified the geometrical demonstrations in order to make his exposition easier to follow. Most important, however, he fleshed out Alhacen’s account of visual perception and cognition by accommodating it to Avicenna’s model of internal senses, thus making explicit the system of psychological faculties that was already implicit in it. ³⁴

John Pecham also found inspiration in Grosseteste but hewed more closely to Alhacen than Bacon in framing his Perspectiva communis (c. 1280). Composed for “the benefit of young students [insofar as] perspective. . . is properly preferred to [all the traditional] teachings of mankind,” ³⁵ this work offers a distillation rather than a compendious treatment of perspectivist optics. When they are provided, mathematical proofs are reduced to the simplest terms, but for the most part Pecham substitutes diagrammatic illustrations for actual mathematical demonstration. Accordingly, the Perspectiva communis gained widespread popularity during the later Middle Ages and Renaissance for the teaching of optics at a rudimentary level.

Whereas both Bacon and Pecham were at pains to avoid the technical complexity of Alhacen’s mathematical demonstrations, Witelo made no such effort in his Perspectiva (c. 1275). On the contrary, he followed Alhacen’s mathematical lead scrupulously while reorganizing the presentation to segment it more clearly into propositional elements, which gave it a tighter, more progressive logical structure in the manner of Euclid’s Elements. With that in mind, Witelo set out a total of 137 introductory propositions in the first book of the Perspectiva before turning to optical matters in the succeeding nine books. As far as the optical content is concerned, Witelo added a few minor details to Alhacen’s account, primarily on the basis of other sources. Thus, after describing Alhacen’s method for measuring angles of refraction from air to water, air to glass, and water to glass, he included Ptolemy’s tabulations and added the reciprocals for refraction in the opposite direction.

Over the course of the later Middle Ages and Renaissance Witelo’s Perspectiva seems to have gained ascendancy over Alhacen’s De aspectibus as the canonical source for perspectivist theory, perhaps because of its theorematic reorganization as well as its coverage of topics not addressed by Alhacen, the rainbow in particular, which the perspectivists added to the Alhacenian optical repertoire. Whatever the case, it saw its first printing in 1535 and its second in a tandem edition with Alhacen’s De aspectibus published by Friedrich Risner in 1572. An optical authority in his own right, Risner made several scholarly improvements and additions to both works that made them far easier to read and digest. This, most likely, was the edition of Witelo’s Perspectiva to which Kepler was responding in the Paralipomena of 1604.

Light, Color, and Rainbow Theory

For the most part, medieval and Renaissance color theory developed along Aristotelian lines. As we saw earlier, Aristotle was far from alone among premodern thinkers in arguing that color is the essential object of sight and, as such, makes external objects visible by defining their basic physical contours. According to this view, color is a real, inherent quality of visible objects, a point agreed upon by virtually every medieval and Renaissance thinker. Aristotle was also far from alone in supposing that all colors are formed from the extremes of black and white in various proportions. As an example, Aristotle points to the fact that when it is seen through thick, darkening haze or smoke, the bright-white sun appears red. ³⁶

The relative proportion of the two extremes determines not only the hue but also the saturation of the resulting color. Thus, the more predominant the white, the brighter and more vivid the color, and vice versa, all within a continuous color-line, or spectrum, stretching from white to black, each point on that line defined by a specific ratio. Since there is an infinitude of such ratios, there is an infinitude of colors along that line. The intensity of light and the quality of the medium through which the color is viewed were also viewed as determinants. “We never see [colors] in absolute purity,” the author of the Pseudo-Aristotelian On Colors asserts. Instead, he goes on, “All hues represent a threefold mixture of light, a translucent medium … and underlying colours from which the light is reflected” ³⁷ A blood-red object seen through a blue transparent medium may appear vivid purple in bright light, but its color will appear murkier and darker as the light dims. Even when seen through perfectly clear air, the apparent color of an object will vary according to the intensity of light illuminating it, so what appears bright red at noon might appear muddy brown at twilight.

If all colors lie in a single, continuous color-line, or spectrum, then we ought not to see clear differentiations among them. Yet we do. The reason, according to Aristotle, is that our inability to discern infinitesimal color-changes leads us to infer gaps between color types. Furthermore, he continues, some colors come to the fore according to the simplicity of the ratio of white to black that determines them. Colors of this sort, Aristotle argues, are “analogous to the sounds that enter into music [so] we may. . . suppose that those involving simple numerical ratios, like the concords in music, may be those generally regarded as most agreeable” ³⁸ In other words, just as a 3:2 ratio provides the pleasing harmony of a perfect fifth in music, a 3:2 ratio of black to white provides a pleasing color. Green, for instance, which is especially pleasing, is presumably formed according to such a simple ratio.

Like the palette of cardinal musical intervals, the palette of cardinal colors is severely limited. In the fourth chapter of On Sense , for instance, Aristotle specifies a set of four such colors in intermediate order from the extremes of white and black—crimson, violet, leek green, and blue—to which he adds “gray” ( phaion ). This he classifies as a variety of black, although it could be regarded as a species of yellow ( xanthos ) in relation to the extreme of white. These colors are primary, according to him, insofar as all others are formed by mixtures among them. Even more limited is the palette of primary colors Aristotle provides in the third book of the Meteorology , where he discusses the formation of the rainbow. Here he narrows the list to three—red, green, and violet—apart from white and black. ³⁹

Several subsequent thinkers, virtually all with philosophical allegiance to Aristotle, disagreed with him about both the color line and the cardinal colors within it. Roger Bacon (d. 1292), for instance, posited seven intermediate colors: lividus (“ivory” or “light grey”), flavus (“light yellow”), puniceus (“orange”), rubeus (“red”), purpureus (“purple” or “violet”), ceruleus (sky blue?), and lazulus (dark azure?). ⁴⁰ Even earlier, Robert Grosseteste (d. 1253) suggested a line of fourteen intermediate colors, all unnamed and each defined by its placement within the scale of white to black, relative brightness, and intensity of illumination. On the Arabic side, Avicenna (d. 1037) settled on the trilogy of red, gray, and blue, thus agreeing with Aristotle’s truncation in the Meteorology but not with his choice of hues. Some two centuries later, Naṣīr al-Dīn al-Tūsī (d. 1274) expanded the scheme to five, which included gray, red, yellow, green, and blue. This is relatively close to Aristotle’s five-color scheme, although it does not include violet.

Whereas both Bacon and Grosseteste accepted a single color-line, Avicenna suggested a three-line color scheme, each line based on white and black at the extremes. One such line passes from white through pale and dark gray to black, another from white through red and red-brown to black, and a third from white through green and indigo to black. This scheme of course reflects his choice of primary colors. Al-Tūsī also adopted a color-line scheme that reflected his choice of primary colors. Accordingly, one line ranges from white through shades of yellow to black, another from white through shades of red to black, another from white through shades of green to black, yet another from white through shades of blue to black, and a final one from white through shades of grey to black. ⁴¹

The spectrum of colors formed by rainbows offers strong support for Aristotle’s basic theory of color insofar as it consists of distinct color bands that blend into one another in a continuum running from vivid red (presumably toward the “white” extreme) to muted blue (presumably toward the “black” extreme). That the intermediate yellow band seems more vivid, and brighter, than its red neighbor would seem to militate against this scheme, but Aristotle explains the problem away by arguing that the yellow is only apparent. In reality, the yellow band appears where the red band overlaps its green neighbor and is thereby “whitened by its juxtaposition” with it. The yellow band, in short, is illusory. Consequently, the number of cardinal colors in the rainbow drops from an apparent four to an actual three: red, green, blue.

For the most part, subsequent thinkers either agreed with Aristotle’s account of the color-bands in the rainbow or modified it only slightly. One exception is the late Renaissance polymath Giambattista Della Porta, who turned Aristotle’s account on its head in book nine of his De Refractione of 1593. For a start, he argued that the red band, not the yellow one, is an illusion caused by the yellow’s contrast with the dark cloud against which it is seen. It therefore appears red, as the sun does when seen through smoke. In addition, he reduced the number of actual colors in the rainbow to two: yellow and blue. The rest, he asserted, are either combinations of these or illusions at either edge of the rainbow created by juxtaposition with the dark cloud. ⁴²

More contentious than the question of what colors define the rainbow was that of how those colors are formed. To this question two basic responses were offered, one based on reflection, the other on refraction. The first alternative was championed by Aristotle, who appealed to reflection from individual drops within the raincloud as the explanatory device. Specifically, he argued that, when the viewer faces the raincloud with the sun to his back, the path of reflection from eye to droplet to sun yields an image that is so small that it is only of the solar color, not of the sun itself. Moreover, as the path of reflection moves downward from the upper, red edge of the rainbow to the lower, blue edge, the longer it gets and the weaker the resulting color, hence the descent from vivid red to duller blue.

Although many subsequent thinkers (Seneca and Roger Bacon among them) followed Aristotle’s lead in taking reflection as the formative principle of the rainbow, several others looked to refraction. Robert Grosseteste, for instance, argued that rainbows are created when sunlight is refracted into the top of the raincloud, where it meets pure air, then to the interior of the cloud, which contains the raindrops, and then out of the raindrops into the posterior part of the cloud, where it presumably forms the spectrum of the rainbow. The raindrops themselves vary in density from rarest at apex to densest at bottom, so it seems to follow that red is produced by refraction through the rarest concentration of raindrops and blue from refraction through the densest concentration. ⁴³ Della Porta offers a somewhat similar explanation, arguing that as the rays of sunlight penetrate the cloud, they are increasingly weakened, appearing brightest at the crimson top of the rainbow and weakest at the violet bottom. ⁴⁴

In both of these cases, the entire raincloud is treated as the medium, not the individual raindrops within the cloud. In the early fourteenth century there were two noteworthy explanations based on refraction through individual raindrops, both similarly argued, and both arrived at independently. One was provided by Kamāl al-Dīn al-Fārisī in his Tanqīḥ , the other by the Dominican friar, Theodoric of Freiberg, in De iride et de radialibus impressionibus (“On the Rainbow and the Impingement of Rays”). Both thinkers relied on experiments with water-filled glass globes in formulating their accounts. And both concluded that the primary bow is formed when rays of sunlight enter the facing, convex surface of the raindrop at particular angles and are refracted to the opposite, concave surface, where they are reflected to the opposite concave surface and then refracted back out into the air. The secondary rainbow is formed by two, rather than one, internal reflection. Thus, the color produced is ultimately contingent on the angle at which the sunlight enters and leaves the raindrop. ⁴⁵

Although both theorists took a significant step toward Descartes’s correct mathematical explanation of the rainbow, which he published in 1637, neither was able to explain why it takes form as an arc. Moreover, despite their partial success in accounting for the phenomenon, neither author seems to have influenced later attempts to explain it. In his discussion of the rainbow in Photismi de Lumine and Umbra (“Elucidating Light and Shadow”), for instance, Francesco Maurolico (d. 1575), attributed the formation of the rainbow to internal reflection within individual raindrops but ignored refraction entirely. Nearly twenty years later, Giambattista Della Porta appealed to refraction alone in his account of the rainbow, but he attributed the formation of the rainbow to refraction through the entire cloud rather than through individual raindrops. ⁴⁶ Descartes, in short, developed his account independent of either Kamāl al-Dīn al-Fārisī or Theodoric.

One peculiarity of the rainbow is that the colors are not actually “in” it, at least not in the way that they are in physical objects such as apples. This point was brought into sharp focus by Roger Bacon, who contended that that, unlike the “real” colors inherent in physical objects, those of the rainbow are only apparent because they are entirely viewer dependent. That is, each viewer sees a rainbow that is unique to his or her viewpoint. He even carried the distinction between real and apparent over to the spectrum of colors produced by prismatic refraction. Even though that spectrum and the one produced by the rainbow are exactly the same, he argued, the prismatic spectrum is real because when it is projected onto a surface, the colors are “fixed” on that surface. In short, their existence is viewer independent. Analogous to the distinction between real and virtual images, the differentiation of real from apparent colors was accepted by virtually everyone until it was abandoned in the seventeenth century. ⁴⁷

Perspectivist Optics and Renaissance Art

Since the 1960s there has been lively debate over the connection between perspectivist optics and the emergence of naturalism in Renaissance art. That many Renaissance artists were versed in perspectivist theory is beyond question. Not beyond question is whether those artists applied this knowledge to the creation of their art, and if so, how they may have done so. The method of one-point perspective is a case in point. Presumably pioneered by Filippo Brunelleschi in the opening years of the fifteenth century, this method was codified by Leon Battista Alberti in his Della pittura (“On Painting”) of 1435.

Figure 19: Alberti’s method of drawing in one-point perspective. Smith, From Sight to Light .

According to Alberti, we start with a rectangle that represents a window through which the painted scene is to be viewed, as in figure 19. We then decide how tall a man should be right at the window, divide that height into three braccia , and subdivide bottom line GF of the rectangle into as many of them as will fit: six in this case. Three of the predetermined braccia above line GF we pick centric point C. This is where the ideal viewer’s visual axis, which Alberti calls the centric ray ( raggio centrico ), reaches through the window into the scene to be painted. Then, from each of the division points on GF we draw a line to C, the resulting set of converging lines representing parallels extended out to infinity. Line CH through the centric point represents the so-called centric line, which demarcates the horizon and is where the top of all figures three braccia tall within the scene will reach.

From point H we extend line HD equal to GF, and from point D we draw lines to each of the division points on GF. From the point of intersection of each of these lines on HF we draw a line parallel to GF. The successive diminution of space between them will represent the diminution of apparent distance as our sight progresses “outward” from GF toward centric line CH. Each trapezoid represents a square seen from the perspective of the ideal viewer, six of them being cut along the diagonal by line EF. Each interval from centric line CH to any of the parallels below it represents the height of a man, as that height diminishes progressively along line AC. ⁴⁸

That Alberti appeals to optical concepts in this construction is obvious from his denomination of the centric ray. This particular ray, according to him, is one of three kinds within the visual cone. Extremal rays ( raggi estremi ) are another kind. They strike the outer boundaries of what we see and thus allow us to judge its size according to the angle at the cone’s vertex. The third kind of rays fill the rest of the visual cone. Styled median rays ( raggi di mezzo ) by Alberti, they convey the object’s surface colors to our eye. The “philosophers,” he informs us, refer to these as “visual rays,” but whether they are emitted by the object or by the eye “is a really difficult controversy that we set aside as completely useless to us.” ⁴⁹ Nonetheless, his overall description smacks far more of Euclid and his fellow visual ray theorists than of Alhacen or any of his perspectivist followers. Nor is it clear whether his method of organizing visual space was founded on theoretical principles drawn from optics or merely vindicated by those principles after the fact.

Leonardo da Vinci offers a clearer example than Alberti not only of a Renaissance artist deeply interested in things optical but also one who seems to have been acquainted, at least to some extent, with perspectivist theory. We know, for instance, that he was familiar with Pecham’s Perspectiva communis , a familiarity that perhaps led him to switch theoretical commitment from extramissionism to intromission in the early 1490s. But he also drew upon works and concepts from other optical and ophthalmological traditions that often led him to significant departures from perspectivist norms. His understanding of the eye and its operation is a case in point.

For a start, rather than place the crystalline lens right at the front of the eye, as perspectivist theory dictates, Leonardo located it at the very center and gave it a spherical rather than oblate shape. In this regard, he seems to have been following contemporary medical authorities rather than perspectivist doctrine. Furthermore, Leonardo recognized that the eye is essentially a camera obscura, its pupil acting as a small aperture through which everything in the field of view radiates its image in inverted order onto the front surface of the lens. The question then was how all that radiation was reinverted as it passed through the lens into the optic nerve in order to reach the brain upright and in proper order. Leonardo sketched several possible ways in which this reinversion could occur, a few of them flouting the laws of refraction so badly as to suggest that Leonardo did not fully understand the phenomenon. In short, his knowledge of perspectivist theory seems to have been limited. ⁵⁰

Adding to the difficulty of pigeonholing Leonardo according to specific optical traditions is that he was an independent and highly innovative thinker. Even when he was wrong, as in the case of his analysis of the eye, he was wrong in interesting and creative ways. Likewise, when he was right, he was right in interesting and creative ways. Take as an example his theory of illumination and shadow casting, which occupies numerous folios among his notebooks. The gist of his theory is illustrated in figure 20, where AC is a light source and EBGDF a body illuminated by it.

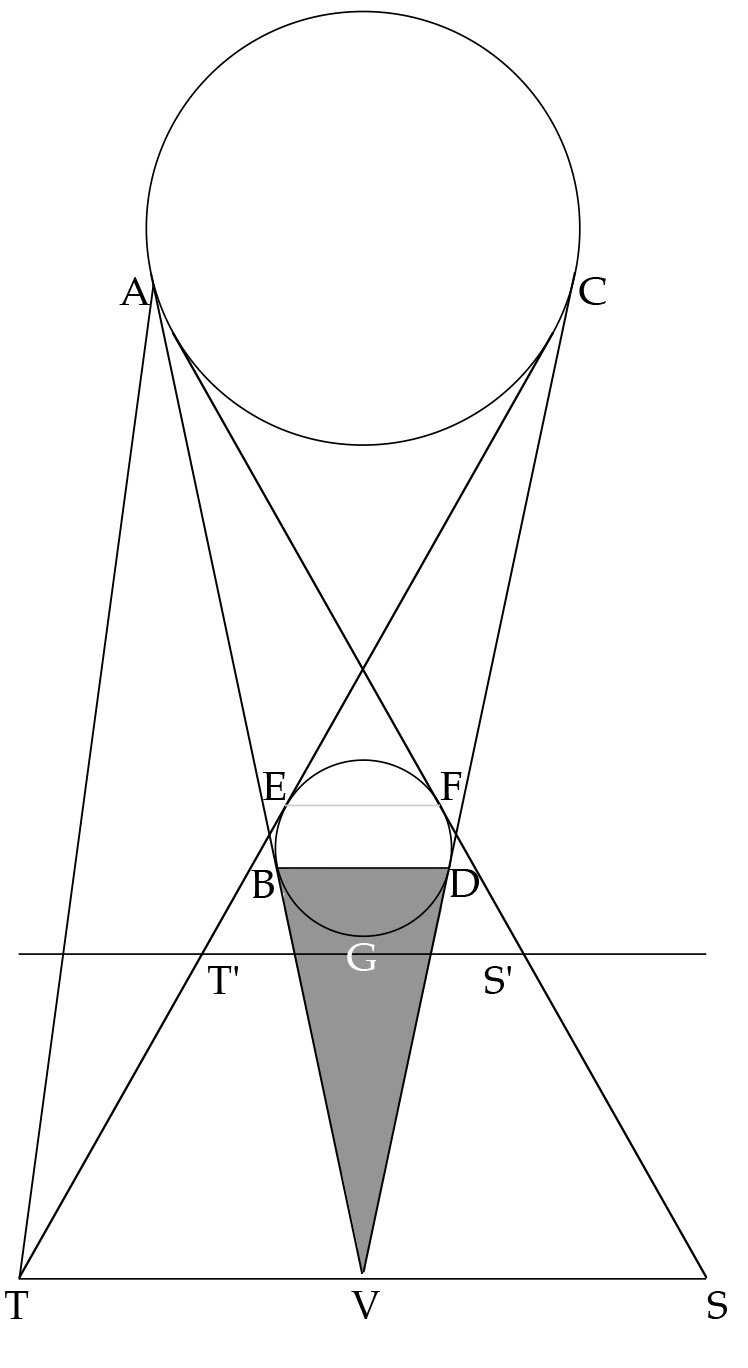
Figure 20: Leonardo da Vinci’s theory of shadow casting. Smith, From Sight to Light .

According to the perspectivists, the shadow cast by the body would be sharply defined by the cone of rays based on A and C at the outer edge of the luminous source that are tangent to the body at B and D and converge at vertex V. Leonardo, on the other hand, realized that shadow would also be cast by radial cones emanating from every point on the luminous source between A and C and forming a base on plane TS. Two such cones are ATV and CTV. It follows, then, that an infinite number of shadows would be cast by an infinite number of such cones upon plane TS to form a circle on it.

But every point on that circle of shadow is open to varying amounts of light from the luminous source. The most intense light reaches points T and S, so it fully counterbalances the shadow there. As we progress inward from T and S toward V, though, the amount of counterbalancing light diminishes because less of the area is open to light. Consequently, the ring of shadow around V becomes ever darker until we reach V itself, where the core shadow, being unadulterated is darkest. Leonardo refers to this core shadow as primitive and the surrounding shadow as derivative, a differentiation that clearly reflects the modern distinction between umbra and penumbra.

Imagine a plane passing through T’ and S’ relatively close to the occluding body. The area on that plane within the dark cone will be in complete shadow, whereas the ring surrounding it will get increasingly lighter as we progress outward toward T’ and S’. As before with T and S, the edge of ring T’S’ surrounding the core shadow will be fully lit by counterbalancing light, and the ring within that edge will get increasingly dark as we progress toward the core shadow. But since that ring is relatively small, the inner ring of penumbral shadow surrounding the core shadow will be small as well. The edge of the core shadow will therefore be relatively sharp but will become increasingly blurred as the plane moves toward V and the penumbral ring increases in size. In short, the farther the plane from the occluding body, the larger the ring of adulterated shadow around the core shadow.

Like the penumbral shadow, the illuminated side of the body varies in brightness according to the amount of light reaching its surface. The most intense illumination is at the very top, which is open to all the light from facing segment AC of the luminous source. As we progress farther down from the top, however, the surface is exposed to less and less light. Accordingly, the surface below line EF will receive none of the light reaching the surface above it, so it will appear less bright. The brightness will continue to diminish as we progress toward BD, where, finally, no light can reach and, therefore, where the core, primitive shadow begins. But line BD does not demarcate a sharp division between light and shadow; rather, that division is blurred by the progressive shadowing that occurs before BD is reached.

This blurring and softening of shadows, both at BD and on planes TS and T’S, is the basis of Leonardo’s painterly technique of sfumato by which he represents the gradual passage from shadow to light on rounded surfaces, such as faces. The connection between optical theory and painterly technique in this case is clear. Far less clear, though, is whether Leonardo conceived that technique from theorizing about shadow casting or whether he discovered it empirically by looking carefully at shadows with his keen eye. If the latter, then the theoretical analysis would have been an after-the-fact vindication of close, practical observation. Whichever the case, Leonardo exemplifies the close relationship between optics and art that evolved during the fifteenth and sixteenth centuries.

Transition to Kepler: 1500-1630

The period between roughly 1450 and 1600 saw several developments, both technological and conceptual, that led to a reconsideration of the perspectivist account of vision, which in turn led to Kepler’s undermining of that account. At the technological level, for instance, the quality of glass improved markedly with the introduction of clear, cristallo glass at Murano in the mid-fifteenth century. Also, as the manufacture of relatively high quality glass spread from Italy to northern Europe during the Renaissance, glass objects became increasingly common and inexpensive. As we will see shortly, one crucial ramification of this expansion of glass production was the manufacture of eyeglass lenses in significant quantity and variety.

No less important than glassmaking, was the printing industry that evolved on the basis of moveable type during the second half of the fifteenth century. This invention allowed for a far wider and more efficient dissemination of scientific knowledge than had been possible during the Middle Ages, when manuscripts were the only means of publication. John Pecham’s Perspectiva communis is a prime case in point. Currently extant in 62 manuscripts, it may have circulated in as many as 1,000 copies between roughly 1280, the probable date of its composition, and 1482/83, when it saw its first printed edition. This is an extremely liberal estimate. On the other hand, between 1482/83 and 1593 it appeared in nine editions or reprintings and one Italian translation. A conservative estimate of the total (at an average print run of 500 per edition) comes to 5,000. Thus, in just over a century, between 1482/83 and 1593, at least five times as many copies of Pecham’s treatise were in circulation as had been available during the two centuries between 1280 and 1482/83. ⁵¹

Among the conceptual developments that led to Kepler’s rejection of perspectivist visual theory, perhaps the most important lay in the reappraisal of Galenic anatomy and physiology during the second half of the sixteenth century and the early years of the seventeenth. Spearheaded by Andreas Vesalius (1514-64), this reappraisal was based at least in part on his hands-on approach to teaching human anatomy and his remarkable observational skills. Having set the standard, Vesalius was followed by a succession of anatomists who continued his critical scrutiny of Galenic doctrine through careful and relatively open-minded dissection of human cadavers. Not only did this scrutiny eventually lead to William Harvey’s demonstration of the circulatory system, but it also led to a reconsideration of the eye and its function in the visual process. The focus here was on the crystalline lens and its relationship to the retina.

Along with these developments, finally, came recognition of certain optical phenomena that had either gone unnoticed or been misunderstood during the Middle Ages. One such phenomenon was the focal property of spherical lenses, which was certainly known during the Middle Ages but improperly analyzed according to incorrect assumptions about refraction. Another such phenomenon was the camera obscura. This device was all but ignored by western thinkers until the beginning of the sixteenth century, when Leonardo da Vinci subjected it to relatively close analysis to determine how it projects inverted images onto a screen. Not only that, but he applied this analysis to the projection of images through the pupil of the eye to the front of the lens. In doing so he took an important first step toward Kepler’s revolutionary theory of retinal imaging.

An Age of Glass

During Roman times, and even earlier, Egypt and Syria were noted for fine glassware. Egypt in particular emerged as a center of production because of the easy availability of natron as a flux to lower the melting temperature of the sand that forms the primary component. Accordingly, by both casting and blowing, Syrian and Egyptian glassmakers were able to manufacture a wide variety of glass objects. Much of the glass, however, was colored either from the addition of colorants or from impurities in the components. One highly prized exception was so-called Alexandrian glass, which was rendered so clear by the addition of antimony that it resembled rock crystal. This, presumably, was the kind of glass used by both Ptolemy and Ibn al-Haytham in their refraction experiments.

With the establishment of the Murano glassworks under Venetian authority at the end of the thirteenth century, glass of more-or-less equivalent quality was produced in Europe. By the mid-fifteenth century a marked improvement in Murano glass came with the invention of cristallo , so-called because its transparency rivalled that of rock crystal. Venice jealously guarded her glass industry both by monopolizing its sources of sand, lime, and flux and swearing its individual manufacturers to secrecy about the tricks of their trade. Not surprisingly, the seal of secrecy soon leaked. As a result, centers of glassmaking sprang up throughout transalpine Europe during the fourteenth, fifteenth, and sixteenth centuries as migrant Venetian craftsmen plied their trade and taught others their secrets.

By the sixteenth century, therefore, glassware of fairly high quality and transparency had become readily available throughout Europe. This development had ramifications for the study of refraction and reflection (through better mirrors), but perhaps its greatest impact was on the manufacture of eyeglasses. Dating from the very late thirteenth century, the earliest eyeglasses were limited to the correction of presbyopia or farsightedness and therefore used convex lenses only. These were normally formed from rock crystal because of its sheer transparency. By the fifteenth century, however, manufacturers could produce glass of adequate transparency to replace rock crystal at lower cost. Consequently, eyeglasses became increasingly affordable and, therefore, increasingly common. Also, the technology of production reached such a point of sophistication by the mid-fifteenth century that convex lenses of varying curvatures were produced to accommodate gradations of presbyopia at five-year intervals between ages thirty and seventy. In addition, concave lenses were ground to accommodate two gradations of myopia. Eyeglasses, in short, were produced almost to prescription for presbyopia, and were available for at least rough correction of myopia. ⁵²

Precisely how eyeglasses improve vision was a mystery because within the medieval optical and ophthalmological tradition poor vision was generally ascribed to a weak flow of visual spirit resulting in only partial innervation of the crystalline lens. Impaired visual acuity was thus thought to be due to the lens’s lack of visual sensitivity, its genesis physiological, not physical in nature. Within this context, improvement by convex lenses made sense because, in magnifying things seen through them, they effectively give a closer look. Concave lenses, on the other hand, present a problem because they make objects look smaller and farther away rather than larger and nearer. They ought therefore to worsen rather than improve defective vision.

Faced with this apparent contradiction in the mid-sixteenth century, Francesco Maurolico sought its resolution in the structure of the eye, specifically the crystalline lens. In line with perspectivist theory, Maurolico assumed that visual impressions made on the front surface of the lens are then passed radially into and through the eye to the opening in the hollow optic nerve. Brought to proper radial “convergence” ( coincidentia ) there, they are then conveyed through the visual spirit permeating the nerve in proper order at the correct size to be perceived clearly. If this convergence occurs too soon or too late, the visual impression will not be perceived clearly.

The culprit in both cases is the curvature of the crystalline lens’s front surface. If the curvature is too sharp, the convergence will occur too soon, whereas if it is not sharp enough, the convergence will occur too late. Either way, the visual impression will not be perceived with appropriate clarity. Premature convergence is optically counteracted by concave lenses, which “spread out” ( disgregant ) the radiation incident on the lens and thus force the convergence to occur later. Delayed convergence, on the other hand, is counteracted by convex lenses, which compress ( congregant) the incident rays so as to force an earlier convergence. ⁵³

This account of how eyeglasses work is a far cry from its modern counterpart. For one thing, it ignores the focal property of the crystalline lens vis-å-vis the retina, and for another, it is firmly ensconced in perspectivist physiological theory with its basis in visual spirit and lenticular sensitivity. Nonetheless, Maurolico’s account points toward modern theory in one crucial way: instead of appealing to physiological causation for impaired vision, Maurolico looked to a physical defect in the eye and, on that basis, proposed a quasi-optical correction according to the refractive properties of convex and concave lenses.

As far as we know, Maurolico’s attempt to explain the functioning of eyeglasses was original; indeed, he seems to have been the first even to make the attempt. He certainly found no precedent in the perspectivist sources, whose analysis of lenses, in the form of glass spheres, is at best rudimentary. For instance, Bacon, Pecham, and Witelo all contend that sunlight passing through a glass sphere will come to convergence at a single point on the side opposite the sun. Maurolico, on the other hand, recognized that such radiation undergoes spherical aberration and, therefore, that it comes to maximum concentration not at a point but, rather, at a spot. He also recognized that when parallel incident rays pass through the sphere, the intersections of the emerging rays form a cone-like figure, but with curved rather than straight sides. Some fifty years later, Kepler opined correctly that this so-called caustic curve might be hyperbolic. ⁵⁴

Although Maurolico was correct about spherical aberration, the shape of the caustic cone, and the fact that the greatest concentration of radial intersections occurs not at a point but at a spot, he made no effort to determine the limit at which that concentration occurs. This limit, which constitutes the so-called focal point, determines the focal length of the sphere as measured on the radial axis from the sphere’s surface. As it turns out, this distance is half the radius of the sphere’s curvature for glass with a reflective index of 1.5, a point demonstrated in the early eleventh century by Ibn al-Haytham in a work on burning spheres that never saw translation.

The first European to address this issue seriously was Giambattista Della Porta, who undertook in his De Refractione of 1593 to determine the focal length of a glass sphere on the supposition that it would be equal to that of a concave spherical mirror. Accordingly, he assumed by analogy that the light exiting the sphere would reach maximum concentration at a distance infinitesimally less than one-half the sphere’s radius. It was of course a matter of pure luck that his determination was correct because its theoretical basis was badly flawed. Nonetheless, what makes his attempt remarkable is that he sought to verify it experimentally by channeling individual rays of sunlight into and through relatively thick plano-convex and plano-concave chunks of glass and tracing their paths to intersection with the axis of radiation.

Figure 21: Della Porta’s experiment for finding the focal point of a semicircular glass lens. Della Porta, De Refractione .

For instance, in figure 21, which is drawn directly from the Latin edition of De Refractione , A, B, C, D, and E mark small holes drilled in the long plate at the top of the diagram. Sunlight is then filtered through those holes through the top surface of the semicircular glass chunk, whence the selected rays follow parallel paths to points of refraction F, G, H, and I at the interface between the glass and the air beyond. From there, they refract toward axis EL, and the farther they strike the convex surface from point L, the higher on axis EL they will intersect it. Thus, refracted ray FR will intersect at a point higher than refracted ray IZ. As the rays strike ever closer to L, then, the closer to the focal point their intersection points with the axis will lie after refraction.

Given the rudimentary nature of the experimental apparatus, this empirical verification would have been too imprecise to invalidate the theoretical model it was meant to test. But its significance lies not in the results but in the fact that it represents a cogent effort to rationalize the study of lenses through a combination of theoretical and empirical ray tracing. In the long run, such efforts to achieve a better understanding of lenticular focusing, along with the ready availability of convex and concave eyeglass lenses, led to the invention and subsequent improvement of telescopes during the first few decades of the seventeenth century. In the slightly shorter run, these same factors were at play in the development of Kepler’s revolutionary theory of retinal imaging.

Looking at Things with New Eyes

As discussed earlier, the perspectivist account of vision was based on an ocular model in which the biconvex crystalline lens is located quite close to the front of the eye with its anterior surface concentric with the eyeball as a whole (see figure 13). Among medieval physicians the prevailing ocular model was markedly different in one respect: the crystalline lens was assumed to be spherical rather than biconvex. Thus, although concentric with the eyeball—also taken to be spherical—its anterior surface was far away from the front of the eye. In virtually every other respect, particularly regarding the tunics of the eye, the hollow optic nerve, and the lens’s sensitivity, the medical and perspectivist models agreed. In short, both physicians and perspectivists based their ocular models on Galenic principles. A key difference between the two was that the physicians tended to favor extramissionism over intromissionism.

By the early sixteenth century, both ocular models came under critical scrutiny because of increasing skepticism about Galenic theory coupled with a new emphasis on close, systematic dissection of human cadavers. Andreas Vesalius (d. 1564) led the way with the publication of his monumental De Corporis Humani Fabrica in 1543. In the anatomical studies leading up to this publication, Vesalius noticed several mistakes Galen had made, in part because Galen depended on comparative anatomy using pigs and barbary apes. Nevertheless, Vesalius was tradition-bound enough to distrust his eyes at times. For instance, despite his inability to find the hollow channel in the optic nerve mandated by Galenic theory, he assumed its existence. Likewise, he failed to recognize that, contrary to the medical tradition of his day, the crystalline lens lies not dead center in the eye but toward the front. He did, however, part ways with the medical tradition of his day in assuming that it is somewhat oblate, not perfectly spherical. He also noticed that it acts like a magnifying glass so that, when held close to a text, it makes the letters larger and easier to read.

Whatever his observational shortcomings, Vesalius set a new standard of precision for anatomical study while encouraging skepticism toward received authority. Following his example, subsequent physicians saw fit to push the crystalline lens away from the center of the eye toward its front while noting its distinctly lenticular rather than spherical shape.

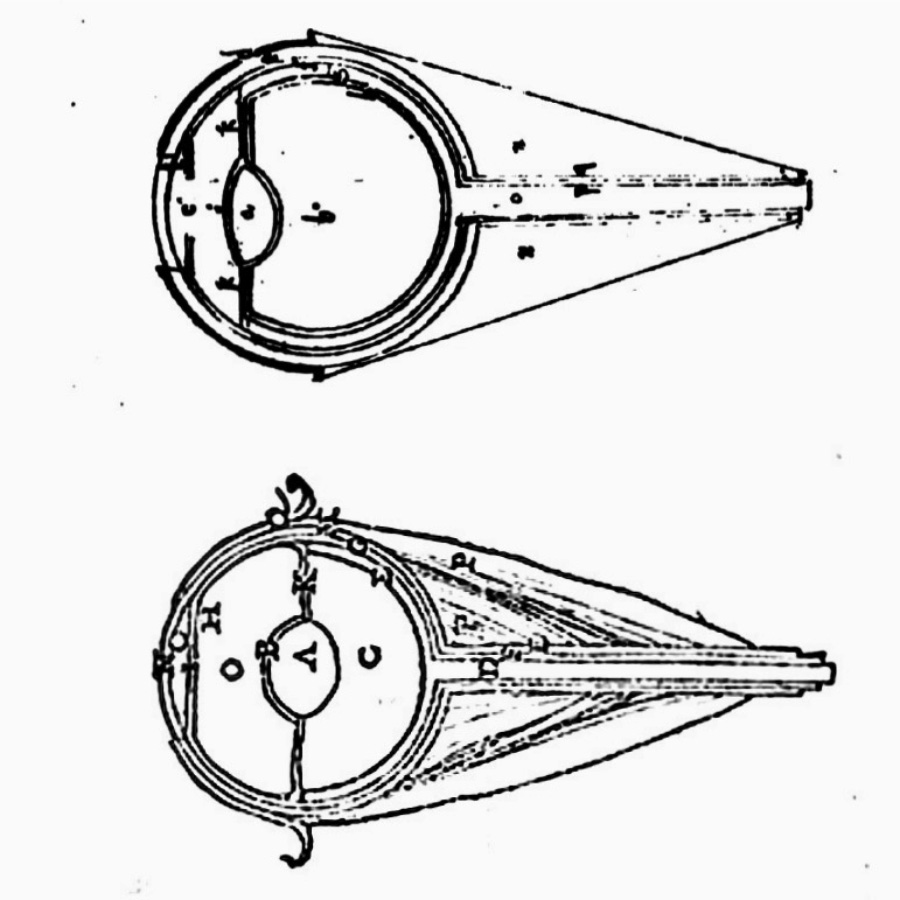
Figure 22: Two anatomical models of the eye, with different placements and shapes of the lens. Vesalius, De Fabrica ; Platter, De Humani Corporis Structura .

These modifications can be seen clearly by comparison in figure 22. The left-hand diagram, which comes from page 643 of Vesalius’s De Fabrica , has the somewhat oblate lens situated at the eyeball’s center. The right-hand diagram comes from tabula 49 of Felix Platter’s De Humani Corporis Structura , which was published forty years after Vesalius’s De Fabrica . Here the lens has not only been pushed forward toward the front of the eyeball—although not nearly far enough—but also flattened in approximation to its actual shape in the eye. Note that in both cases the optic nerve lies directly along the eye’s axis, even though in reality it is displaced several degrees from it. That both physicians retained this axial placement indicates their continuing (if perhaps reluctant) agreement that the optic nerve serves as a conduit for visual spirit.

The anatomical structure of the eye was not the only thing at issue during the sixteenth century. How the eye functions in vision was also under critical review. One of the earliest and most remarkable revisions to the traditional view of ocular function was proposed by Leonardo da Vinci in the very early 1500s. As far as ocular anatomy and physiology are concerned, Leonardo followed the medical tradition in three critical ways. First, he assumed that the crystalline lens is perfectly spherical and concentric with the spherical eyeball. Second, he located the optic nerve along the eye’s axis and took it to be pipeline for visual spirit flowing to the lens from the brain. Third, he accepted that the lens, more specifically its anterior surface, is the seat of visual sensitivity. Against the medical tradition, he was a proponent of intromissionism.

In the 1480s Leonardo had noticed that if a small hole is punched in the wall of an enclosed, dark room facing a brightly lit scene, that scene will be projected through the hole onto the back wall of the room in reversed and inverted order. This, of course, is the camera obscura , and Leonardo soon realized that the eye, with its small pupillary opening into the dark uveal basin is an example. This realization also led him to break ranks with the physicians in rejecting extramisionism. Accordingly, he maintained that the radiation from every point outside the eye enters through the pupil to reach a point on the opposite side of the lens’s facing surface. In other words, a ray from the rightward side of the scene will reach a leftward point on the lens and vice-versa throughout. When all such radiation is taken into account, therefore, it projects a reversed and inverted image on the lens’s anterior surface. The problem is that we see things upright, not inverted, so Leonardo reasoned that the image projected upon the front of the lens had somehow to be re-inverted by the lens in such a way as to reach the hollow optic nerve in upright order and in precisely the right size to enter it. Such an optical reinversion is in fact impossible according to the principles of refraction, and Leonardo’s attempt to force it indicates his rather sketchy understanding of optics at the technical level. ⁵⁵

Like Leonardo decades before him, Giambattista Della Porta was fascinated by the projection of images in a camera obscura , which he discusses at some length in book 17, chapter 6 of the 1589 edition of his Magiae Naturalis . In the course of this discussion, he notes that placing a convex lens just behind the small aperture renders the image projected on the back wall or a white screen clearer and more vivid. Subsequently, he remarks that the eye, with its pupillary opening, operates like a camera obscura , projecting the external scene in reversed and inverted order onto the anterior surface of the crystalline lens. ⁵⁶ This point is echoed four years later in De Refractione : “I say that just as the light shining through a narrow window onto paper . . . represents objects illuminated by the Sun, so it depicts the images of visible things by shining through the opening of the pupil and falling onto the crystalline humor.” ⁵⁷

According to his observation of a camera obscura furnished with a convex lens, Della Porta should have concluded that these images are projected by the crystalline lens onto the retinal wall at the back of the eye. That he failed to reach this conclusion was due to his firm belief that the lens is visually sensitive and, as such, channels the image formed on its anterior surface into the hollow optic nerve. Consequently, Della Porta had to find a way to ensure that the image enters the optic nerve upright. To this end, he supposed that each spot on the anterior surface of the lens forms a particular viewpoint. Hence, when a luminous or illuminated spot outside the eye projects a ray to any such viewpoint, it sees that external spot at its proper location in terms of horizontal and vertical direction. In the aggregate, all such viewpoints will therefore see the composite of all such external points in their proper location according to their proper orientation. ⁵⁸

Whereas Leonardo da Vinci and Giambattista Della Porta were unable to break with tradition in their understanding of the crystalline lens and its sensitive function, Felix Platter felt no such constraints. Quite the contrary, he had no qualms about transposing visual sensitivity from the crystalline lens to the optic nerve and its retinal extension, thus reducing the lens to magnifying glass and the eye to a true camera obscura . “The primary component of the eye,” he argues, “which is the optic nerve, is spread out into a concave retiform hemisphere after it enters the eye [at the rear].” This retiform hemisphere, he continues, “takes on and distinguishes the shapes and colors of external things, which flow along with the light into the eye through the aperture of the pupil and are displayed on it by its lens, as will be confirmed.” The confirmation comes with the claim that the lens “collects all the rays [that enter the pupil], so as to propagate them throughout the entire ambit of the retiform nerve.” ⁵⁹ In other words, the lens casts an image of the external world onto the retina.

With Platter’s revised understanding of ocular function, the grounds were fully laid for Kepler’s theory of retinal imaging. The argument that the eye functions as a camera obscura furnished with a biconvex lens (as described by Giambattista Della Porta) was cogently laid out. The anatomical model that supported the argument was well established. The laws of refraction that determined the optics of the eye were firmly instituted, at least qualitatively. And the focal property of biconvex lenses was fairly well understood. At a technical level, therefore, all that remained for Kepler to do was tie loose ends.

Kepler: At Loose Ends

Kepler’s Ad Vitellionem Paraliomena was the fruit of several years of close study aimed at understanding the observational grounds of astronomy according to the instruments used to determine celestial motions and positions. One such instrument, of course, was the camera obscura , which was used for the observation of solar and lunar eclipses. Kepler analyzed it in detail in chapter 2 of the Paralipomena . Another such instrument is the eye itself, which Kepler took to be a sort of camera obscura . He was inclined to this assumption by his reading and approval of Della Porta and, more to the point, Platter, but he also recognized the conceptual and practical shortcomings of their accounts. Thus, his own analysis of the eye and its operation in chapter 5 of the Paralipomena was intended to overcome those shortcomings.

Key to properly understanding ocular function, Kepler realized, was understanding the optics of the crystalline lens. Accordingly, he turned first to a mathematical analysis of light rays passing through a transparent sphere from various points outside it. On that basis he showed how parallel rays are brought to a focal concentration after exiting the sphere and undergoing spherical aberration. He also showed how the resulting focal area can shift depending on how close or how distant the light source is from the sphere. The closer the source, he concluded, the more distant the focal area, and vice-versa. ⁶⁰

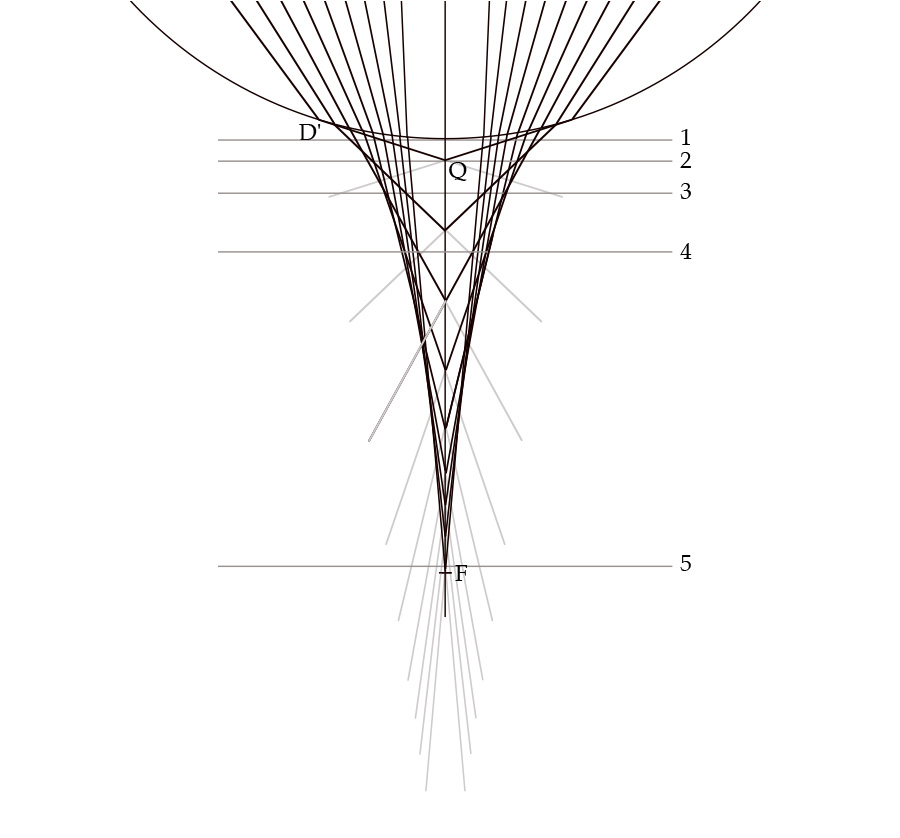
Figure 23: Kepler’s experiment for investigating the focal point of a spherical lens. Smith, From Sight to Light .

With these points in mind, Kepler turned to an empirical test of his conclusions. For this purpose, he used the spherical base of a urinary flask filled with water to represent the crystalline lens. Through it he passed a shaft of sunlight consisting of myriad parallel rays, as illustrated in figure 23, where the axis of the sphere passes through point Q and symmetrical sets of rays refract toward the axis through the sphere’s lower surface. These rays result from the refraction of parallel rays through the sphere’s top, which is not pictured. The ray that refracts through D’ meets its mate on the other side at Q on the axis. Rays to the left of D’ and to the right of its mate on the other side will not refract out of the sphere to meet the axis. Meantime, the matching sets of rays between D’ and Q, and their counterparts on the other side, will intersect the axis at successively lower points between Q and F. The densest concentration of intersections occurs just above F, which is the focal point. After this point, the light suddenly disperses while becoming ever weaker.

With all this in mind, Kepler tells us that he held a sheet of paper up against the spherical base tangent to the axis at the position represented by line 1 in figure 23. Then he slowly moved the paper downward through positions 2, 3, 4, etc., noting that at each position a relatively bright ring with a relatively bright luminous spot in the center is formed on the paper, each ring getting progressively smaller at a decelerating rate. Finally, at position 5, the ring and central dot merge to form the focal spot. This of course is where the intersections are at their densest and, according to him, where the sunlight is concentrated enough to ignite gunpowder. From this experiment Kepler concluded that the ring of light at each level on the curved cone of intersections is caused by non-matching rays that intersect to form the cone’s surface. ⁶¹

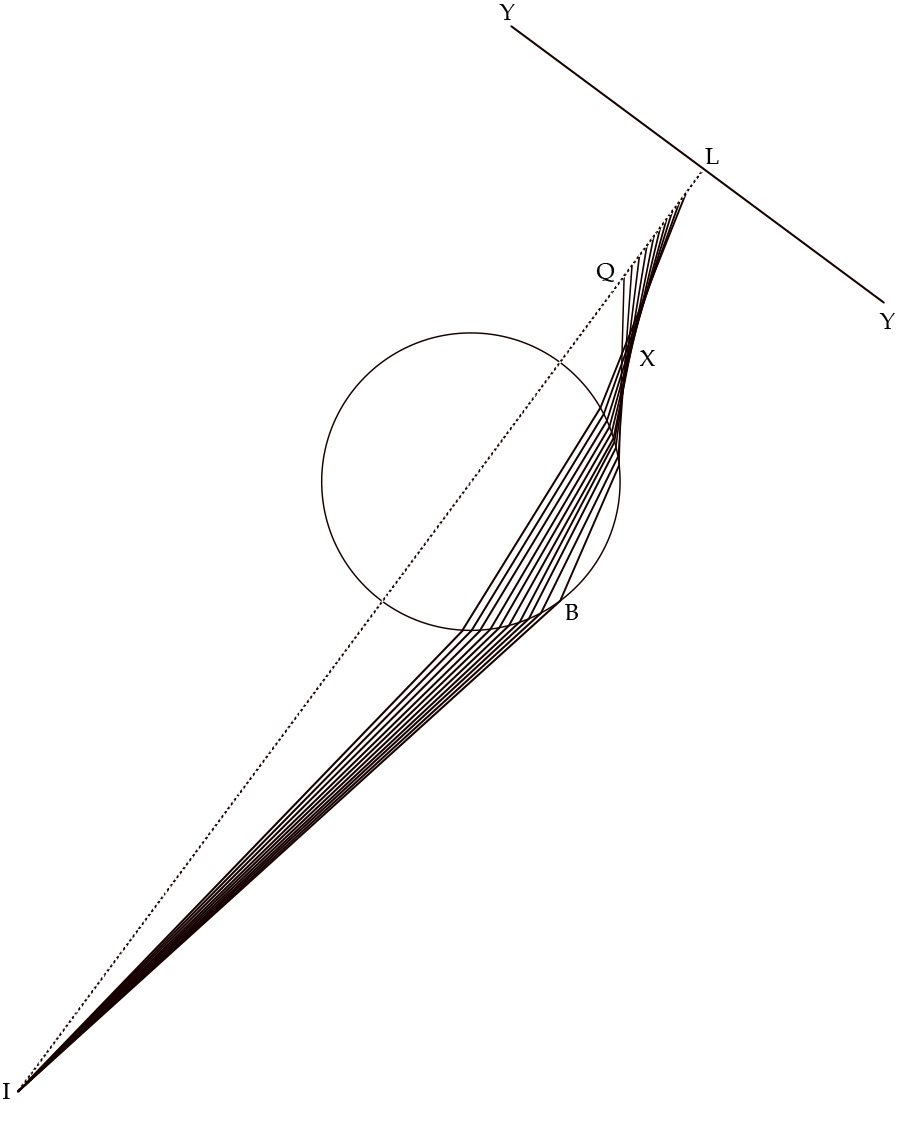
Figure 24: Kepler’s illustration of light refracting through a spherical lens, with an area of high concentration identified. Smith, From Sight to Light .

Now let us take single point I of light in figure 24. It radiates to all the facing points of the sphere represented by the circle to form a cone with axis IQ. After exiting the sphere, the rays will come to a focus at point L to form a bright spot of light on sheet of paper XY held there. If we concentrate our analysis only on the outer rays from I, then we see two things. First, the farther to the right the ray, the closer to the sphere it intersects the axis. Consequently, the ray entering at B farthest to the right meets the axis at point Q closest to the sphere. Second, where all the exiting rays cross, marked by X, represents an area of relatively high concentration and, therefore, relatively bright illumination.

Figure 25: Kepler’s discussion of light refracting through a lens after it passes through a small perforation. Smith, From Sight to Light .

The implications of this analysis come clear in figure 25, where two points of light, I and I’ face the lens well to the left and right of axis HK. DG is a diaphragm with a narrow perforation at EF which screens most of the light from I and I’, allowing only thin shafts to reach the lens. As both shafts are refracted through the sphere toward the lens’s focal point, their constituent rays cross at points M and M’, where the light is relatively heavily concentrated. The same analysis will hold for other luminous points outside the sphere and far to the sides of axis H. Their constituent rays within the thin shafts channeled through perforation EF will cross to form areas of concentrated light. In the aggregate, these areas lie on a curve whose point K is the focal point for light radiating from H. Light radiating from points X and Y relatively close to H on either side will also come to focus on that curve. Hence, the light radiating from every point outside the sphere through the perforation in the diaphragm will be projected to corresponding points on this curve.

This, of course, is how the Keplerian eye, with its pupillary opening and lens, functions in order to cast an image of the external world onto the retinal screen. It is also why the eye is structured as it is. For one thing, the roughly hemispherical shape of the retinal screen allows for an extraordinarily wide field of view to be projected onto it. For another thing, this shape allows the projected image a far greater area of focal clarity than does a flat wall or screen. For yet another thing, it explains how eyeglasses work by correcting refractive disorders due to the incoming light’s focal points lying either in front of the retinal screen or behind it. In the former case, which occurs in nearsightedness or myopia, concave lenses push the focal points back to the retina’s surface. In the latter case (i.e., farsightedness or presbyopia), convex lenses bring the focal points forward to the retina’s surface. ⁶²

The virtue of Kepler’s theory is its explanatory scope and power. But it has two distinct drawbacks in comparison to the perspectivist alternative. First, the image cast on the retina is inverted, and there is no clear mechanism, optical or otherwise, for reinverting it. In response to this issue, Kepler argued that “even if from a universal perspective” the image is reversed and inverted, “nevertheless, the right parts of the object are perfectly opposed to the right parts of the picture, and the upper parts of the object to the upper parts of the picture” according to connecting lines that intersect at the center of the eye. This would not be the case if the image were upright, “for then the interior wall of the eye would in some places be directly opposite the object, in others not.” ⁶³ In short, the reversed and inverted “picture” and its objective source are symmetrically aligned.

The second drawback involved the status of the retinal image, which Kepler called a pictura (“painting”) in order to distinguish it from the imago (“image”) that was supposed to pass from the crystalline lens into the brain according to perspectivist theory. As Kepler describes it, an imago “is, for the most part, a virtual entity, a product of vision.” As a result, “when the act of seeing ceases, the image goes out of existence.” ⁶⁴ Kepler’s picturae , on the other hand, “really exist on paper or other surfaces.” ⁶⁵ As such, they are viewer independent. Thus, to put it simply, imagines are realized subjectively, picturae objectively. One is a purely psychological creation, the other a purely physical creation.

How, then, are such objective representations seen? That they are unsuited to the physiological process of perspectivist visual theory seems clear enough. To start with, they are far too large to fit through the optic nerves and reach into the brain for perceptual discrimination. Being real and physical, moreover, they are incompatible with visual spirit, which is specific to the conveyance of virtual representations, in the form of species. Also, whereas the formation of Kepler’s pictura is subject to the physical laws of light-radiation, the transmission of perspectivist imagines through the eye and the windings of the optic nerves into the brain flouts those laws.

Faced with the obvious incompatibility between his physical theory of retinal “picturing” and the prevailing theory of species-based sensation and perception, Kepler was at a loss to explain how the two might be accommodated to one another, if at all. Perhaps the visual spirit pervading the retina “sees” the pictura projected on it and conveys the impression back into the brain. Or perhaps the visual power sends something out to look at the pictura and report what it “sees” back to the perceptual faculty in the brain. Whatever the case, Kepler refused to take a stand, leaving it “to the natural philosophers to argue about” the explanation. “For,” as he maintained in vindication of his refusal, “the arsenal of optical writers does not extend beyond [the] opaque wall” of the retina. ⁶⁶

By signaling the difference between “optical writers,” whose task is to explain ocular function at the physical level, and “natural philosophers,” who are to account for visual processing at the physiological and psychological level, Kepler pointed toward the modern distinction between physical optics and physiological optics. Implicit in this distinction, as articulated by Kepler, was that physiological optics is subservient to physical optics and, therefore, that any theory of visual processing had to accommodate itself to physical light- and color-theory. This marked a significant reversal in the hierarchical order of perspectivist optics, where physical light- and color-theory were subservient to the theory of visual processing.

Conclusion

Kepler’s theory of retinal imaging marked a critical turning point toward the modern in the evolution of both physical and physiological optics. During the century that followed the publication of his Paralipomena , light- and color-theory underwent a radical transformation based on the physical interaction of particles, all within the context of the so-called mechanical philosophy. Among the key figures in this transformation were René Descartes (d. 1650), Robert Hooke (d. 1703), Christiaan Huygens (d. 1695), and Isaac Newton (d. 1727).

At the technical level there followed a vastly improved understanding of light and its physical manifestations, especially in regard to refraction and diffraction. This understanding in turn led to significant improvements in telescopy, which was put on a scientific footing by Galileo when he aimed his instrument at the night sky in 1609. Likewise, microscopy came into its own during the second half of the seventeenth century, one crucial advance being the development of the compound microscope by Robert Hooke and the publication of his microscopic observations in the Micrographia of 1665.

Meantime, in conjunction with the effort to mechanize the physics of light and color came an effort to mechanize the entire visual process from sensation to perception and cognition. Instrumental in this effort was Descartes, who explained the visual system in more-or-less hydraulic terms, starting with the assumption that each point on the retina is connected to a particular filament running through the optic nerve to the forefront of the brain. Thus, when the Keplerian pictura is projected onto the retina, each point on that pictura activates one of those filaments mechanically. The mechanical effect is then conveyed through the filament to the front of the brain, where it ends up making a physical impression on the pineal gland in the brain’s center. Altogether these effects are mapped onto the pineal gland in a way that corresponds to the original pictura . However, as Descartes is quick to add, this mapping is not itself an image, and certainly not an imago in the perspectivist sense. ⁶⁷

Problematic to be sure, Descartes’s mechanistic approach to visual theory, in all its ramifications, nonetheless proved foundational for visual theory throughout the Enlightenment, albeit with various modifications, as the understanding of vision and its physical basis became more sophisticated. It also put paid to perspectivist optics and its theoretical foundations in species-theory and the physiology of spirits. Indeed, by the late seventeenth century the entire theoretical apparatus of perspectivist theory had been rendered obsolete. All told, then, the ostensibly minor step of shifting the visual image from crystalline lens to retina had monumental consequences for both physical and physiological optics.

Bibliography

Ackerman, James. “Leonardo’s Eye.” Journal of the Warburg and Courtauld Institutes 41 (1978): 108-46. ( Link to IsisCB )

Alberti, Leon Battista. On Painting. Translated by Rocco Sinisgalli. Leon Battista Alberti : On Painting. Cambridge, New York: Cambridge University Press, 2011.

Alhacen. De aspectibus , 1-3. Edited and translated by A. Mark Smith. Alhacen’s Theory of Visual Perception: A Critical Edition, with English Translation and Commentary, of the First Three Books of Alhacen’s De Aspectibus, the Medieval Latin Version of Ibn al-Haytham’s Kitāb al-Manāẓir . Transactions of the American Philosophical Society 91.4 and 91.5. Philadelphia: American Philosophical Society Press, 2001. ( Link to IsisCB )

Alhacen. De aspectibus , 4-5. Edited and translated by A. Mark Smith. Alhacen on The Principles of Reflection: A Critical Edition, with English Translation, Introduction, and Commentary, of Books 4 and 5 of Alhacen’s De aspectibus, the Medieval Latin Version of Ibn al-Haytham’s Kitāb al-Manāẓir. Transactions of the American Philosophical Society 94.2 and 94.3. Philadelphia: American Philosophical Society Press, 2006. ( Link to IsisCB )

Alhacen. De aspectibus , 7. Edited and translated by A. Mark Smith. Alhacen on Refraction: A Critical Edition, with English Translation, Introduction, and Commentary, of Book 7 of Alhacen’s De aspectibus, the Medieval Latin Version of Ibn al-Haytham’s Kitāb al-Manāẓir. Transactions of the American Philosophical Society 100.1 and 100.2. Philadelphia: American Philosophical Society Press, 2010.

Anthemius of Tralles. Περί παραδόξων μηχανημάτων . Translated by George L. Huxley. Anthemius of Tralles: A Study in Later Greek Geometry . Cambridge, MA: Easton Press, 1959.

Aristotle. Meteorology. Translated by E. W. Webster. In The Complete Works of Aristotle , vol. 1, edited by Jonathan Barnes, 555-625. Princeton: Princeton University Press, 1984. ( Link to IsisCB )

Aristotle. On Sense and What Is Sensed . Translated by J. I. Beare. In The Complete Works of Aristotle , vol. 1, edited by Jonathan Barnes, 693-713. Princeton: Princeton University Press, 1984. ( Link to IsisCB )

Aristotle. On the Soul . Translated by J. A. Smith. In The Complete Works of Aristotle, vol. 1, edited by Jonathan Barnes, 641-92. Princeton: Princeton University Press, 1984. ( Link to IsisCB )

Bacon, Roger. Opus majus . Translated by Robert B. Burke. The Opus Majus of Roger Bacon, vol 2 . Philadelphia: University of Pennsylvania Press, 1928.

Bacon, Roger. Perspectiva. Edited and translated by David C. Lindberg. Roger Bacon and the Origins of Perspectiva in the Middle Ages: A Critical Edition and English Translation of Bacon’s Perspectiva with Introduction and Notes . Oxford: Clarendon Press, 1996. ( Link to IsisCB )

Barnes, Jonathan, ed. The Complete Works of Aristotle. 2 vols. Princeton: Princeton University Press, 1984. ( Link to IsisCB )

Baur, Ludwig, ed. Die Philosophischen Werke des Robert Grosseteste, Bischofs von Lincoln . Münster: Aschendorff, 1912. (Link to IsisCB)

Boyer, Carl B. “Theory of the Rainbow: Medieval Triumph and Failure.” Isis 49 (1958): 378-90.

Della Porta, Giambattista. De refractione . Edited and translated by A. Mark Smith. Optical Magic in the Late Renaissance: Giambattista Della Porta’s De Refractione of 1593 . Transactions of the American Philosophical Society 107.1. Philadelphia: American Philosophical Society Press, 2019.

Della Porta, Giambattista. Magiae Naturalis Libri XX. Naples, 1589.

Diocles. On Burning Mirrors. Translated by Gerald J. Toomer. Diocles on Burning Mirrors. Berlin, New York: Springer, 1976. ( Link to IsisCB )

Euclid. Optics and Catoptrics. Edited and translated by I. L. Heiberg. Euclidis Opera Omnia, vol 7 . Leipzig: Teubner, 1895.

Galen . De usu partium. Translated by Margaret Tallmadge May. Galen on the Usefulness of the Parts of the Body, vol 2. Ithaca, NY: Cornell University Press, 1968. ( Link to IsisCB )

Galen. On the Doctrines of Hippocrates and Plato. Translated by Phillip DeLacey. Berlin: Akademie Verlag, 1980. ( Link to IsisCB )

Grant, Edward, ed. A Source Book in Medieval Science . Cambridge, MA: Harvard University Press, 1974. ( Link to IsisCB )

Gutas, Dimitri. Greek Thought, Arabic Culture . London, New York: Routledge, 1998. ( Link to IsisCB )

Harvey, Joshua, Hannah Smithson, Clive Siviour, Giles E. M. Gasper, Sigbjorn O. Sonnesyn, Brian K. Tanner, and Tom McLeish. “Bow-Shaped Caustics from Conical Prisms: A 13th-Century Account of Rainbow Formation from Robert Grosseteste's De iride .” Applied Optics 56 (2017): G197-G204.

Hero. Catoptrics . Edited and translated by L. Nix and W. Schmidt. Heronis Alexandrini Opera Quae Supersunt Omnia, vol. 2.1. Leipzig: Teubner, 1900.

Ilardi, Vincent. Renaissance Vision from Spectacles to Telescopes. Philadelphia: American Philosophical Society Press, 2007. ( Link to IsisCB )

Kepler, Johannes. Ad Vitellionem Paralipomena . Translated by William Donahue . Optics: Paralipomena to Witelo and Optical Part of Astronomy. Santa Fe, NM: Green Lion Press, 2000. ( Link to IsisCB )

Kirchner, Eric. “Color Theory and Color Order in Medieval Islam: A Review.” Color Research and Application 40 (2015): 5–16. http://onlinelibrary.wiley.com/wol1/doi/10.1002/col.21861/full .

Maurolico, Francesco. Photismi De Lumine, et umbra ad perspectivam, et radiorum incidentiam facientes . Naples, 1611.

McCray, W. Patrick. Glassmaking in Renaissance Venice: The Fragile Craft . Aldershot, UK, Burlington, VT: Ashgate, 1999. ( Link to IsisCB )

Parkhurst, Charles. “Roger Bacon on Color: Sources, Theories & Influence.” In The Verbal and the Visual: Essays in Honor of William Sebastian Heckscher, edited by Karl-Ludwig Selig and Elizabeth Sears, 151-201 . New York: Italica Press, 1990. ( Link to IsisCB )

Pecham, John. Perspectiva communis . Edited and translated by David C. Lindberg. John Pecham and the Science of Optics. Madison: University of Wisconsin Press, 1970.

Plato. Timaeus . Translated by Donald Zeyl. Plato Timaeus. Indianapolis: Hackett, 2000. ( Link to IsisCB )

Platter, Felix. De Corporis Humani Structura et Usu . Basel, 1583.

Pseudo-Aristotle. On Colours. Translated by T. Loveday and E. S. Forster. In The Complete Works of Aristotle, vol. 1, edited by Jonathan Barnes, 1219-28. Princeton: Princeton University Press, 1984. ( Link to IsisCB )

Ptolemy. Optics. Translated by A. Mark Smith. Ptolemy and the Foundations of Ancient Mathematical Optics . Transactions of the American Philosophical Society 89.3. Philadelphia: American Philosophical Society Press, 1999. ( Link to IsisCB )

Rashed, Roshdi. “A Pioneer in Anaclastics: Ibn Sahl on Burning Mirrors and Lenses.” Isis 81 (1990): 464-91. ( Link to IsisCB )

Richardson, William Frank and John Burd Carman, trans. Vesalius On the Fabric of the Human Body, Books III and IV . Novato, CA: Norman Publishing, 2002.

Risner, Friedrich, ed. Opticae Thesaurus . Basel, 1572.

Smith, A. Mark. “Alhacen’s Approach to ‘Alhazen’s Problem.’” Arabic Sciences and Philosophy 18 (2008): 143-63. ( Link to IsisCB )

Smith, A. Mark. From Sight to Light: The Passage from Ancient to Modern Optics . Chicago: University of Chicago Press, 2015. ( Link to IsisCB )

Smith, A. Mark. “Ptolemy’s Search for a Law of Refraction: A Case-Study in the Classical Methodology of ‘Saving the Appearances’ and Its Limitations.” Archive for History of Exact Sciences 26 (1982): 221-40. ( Link to IsisCB )

Vesalius, Andreas. De humani corpors fabrica libri septem. Basel: 1543 .

---

1. Plato, Timaeus , 33, 45-47, 61. ↩

2. Aristotle, On the Soul , 665-67, 675-77, 691. ↩

3. For an overview of Euclid’s theory, see Smith, Sight to Light , 47-55. ↩

4. Adapted from Euclid, Optics , 178-79. ↩

5. Hero, Catoptrics , 324­-30. ↩

6. Ptolemy, Optics , 70. On the problematic manuscript tradition of the Optics , see 5-11. ↩

7. Ptolemy, Optics , 72. ↩

8. For Ptolemy’s account of the grounds of vision, see Optics , 71-82, 90-106. ↩

9. Ptolemy, Optics , 106-28, 119, 151. ↩

10. Ptolemy, Optics , 82-86. ↩

11. Ptolemy, Optics , 132-38. ↩

12. Ptolemy, Optics , 194-95, 206-7. ↩

13. Ptolemy, Optics , 229. ↩

14. Ptolemy, Optics , 231-37. See also Smith, “Ptolemy’s Search for a Law of Refraction.” ↩

15. Ptolemy, Optics , 238-42. ↩

16. Ptolemy, Optics , 257. ↩

17. Galen, De usu partium , 463-81, 491-503; also, Galen, On the Doctrines , 448-62; for an overview, see Smith, From Sight to Light . ↩

18. Euclid, Catoptrics , 340-42. ↩

19. Diocles, On Burning Mirrors . ↩

20. Anthemius, Περί παραδόξων , 6-9, 17-18. ↩

21. Gutas, Greek Thought, Arabic Culture . ↩

22. Rashed, “A Pioneer in Anaclastics.” ↩

23. For an overview of Avicenna’s account, see Smith, Sight to Light , 159-66. ↩

24. Alhacen, De aspectibus , 1-3 (91.5), 343-48. ↩

25. Alhacen, De aspectibus , 1-3 (91.5), 348-55. ↩

26. Alhacen, De aspectibus , 1-3 (91.5), 355-69. ↩

27. Alhacen, De aspectibus , 1-3 (91.5), 417-529; for an overview of Ibn al-Haytham’s entire account, see Smith, From Sight to Light , 181-94. ↩

28. Alhacen, De aspectibus , 7 (100.3), 325-30. ↩

29. Alhacen, De aspectibus , 4-5 (96.3), 300-17. ↩

30. Alhacen, De aspectibus , 4-5 (96.3), 385-94. ↩

31. For an analysis of Alhacen’s solutions to “Alhazen’s Problem,” see Smith, “Alhacen’s Approach to ‘Alhazen’s Problem.’” For Ptolemy’s contribution, see Optics , 182-85. ↩

32. Alhacen, De aspectibus , 7 (100.3), 220-60. ↩

33. Baur, Philosophischen Werke , 59-65; translation, adapted from Grant, Source Book in Medieval Science , 385-87. ↩

34. Bacon, Perspectiva , 3-27, esp. 5-17. ↩

35. Pecham, Perspectiva communis , 61. ↩

36. Aristotle, On Sense , 697-700. ↩

37. Pseudo-Aristotle, On colours , vol. 1, 1222. ↩

38. Aristotle, On Sense , 698. ↩

39. Aristotle, Meteorology , 603-4. ↩

40. Parkhurst, “Roger Bacon on Color.” ↩

41. Kirchner, “Color Theory and Color Order.” ↩

42. Della Porta, De Refractione , 397-405. ↩

43. Harvey et al., “Bow-Shaped Caustics.” ↩

44. Della Porta, De Refractione , 411-13, 417-18. ↩

45. Boyer, “Theory of the Rainbow.” ↩

46. Maurolico, Photismi, 49-55; Della Porta, De Refractione , 411. ↩

47. Bacon, Opus majus , 604-5; also, Della Porta, De Refractione , 434-37. ↩

48. Alberti, On Painting , 27-30, 39-42. ↩

49. Alberti, On Painting , 26. ↩

50. Ackerman, “Leonardo’s Eye.” ↩

51. Pecham, Perspectiva communis , 52-58. ↩

52. Ilardi, Renaissance Vision . ↩

53. Maurolico, Photismi , 73-80. ↩

54. Maurolico, Photismi , 40-46. ↩

55. Smith, From Sight to Light , 305-8. ↩

56. Della Porta, Magiae Naturalis , 266-67. ↩

57. Della Porta, De Refractione , 193-94. ↩

58. Della Porta, De Refractione , xlix-lii. ↩

59. Platter, De Structura , 186. ↩

60. Kepler, Paralipomena (2000), 196-210. ↩

61. Kepler, Paralipomena (2000), 210-15. ↩

62. Kepler, Paralipomena (2000), 216-18. ↩

63. Kepler, Paralipomena (2000), 221. ↩

64. Kepler, Paralipomena (1604), 180 (my translation). ↩

65. Kepler, Paralipomena (2000), 210. ↩

66. Kepler, Paralipomena (2000), 180. ↩

67. Smith, From Sight to Light , 409-15. ↩

KEYWORDS

1. sight
2. light
3. geometry